이득우의 게임 수학
멱급수가 수렴하기 위한 조건을 알아봤으니, 이제 무한번 미분 가능한 함수를 멱급수 형태로 바꾸는 방법에 대해 알아본다.
- 이러한 멱급수를 매클로린 급수 혹은 테일러 급수(Taylor series)라고 한다.
수렴하는 멱급수에서 공비 r을 x로 바꿔 f(x)로 정의한다.
어떤 함수가 무한번 미분 가능하다면, 멱급수의 도함수는 다음과 같이 전개될 것이다.
x에 0을 대입하면, 멱급수를 구성하는 각 항의 계수 a.n과 일정한 규칙을 가지는 상수만 남는다.
위 식들은 계승(Factorial)을 사용해 다음과 같이 간단히 표기할 수 있다.
멱급수의 n번째 계수 a.n은 다음과 같이 나타낼 수 있다.
멱급수 전개는 다음과 같이 n번 미분한 도함수에 0을 대입한 형태로 일반화할 수 있고, 이를 매클로린 급수 또는 테일러 급수라고 한다.
- 매클로린 급수는 무한급수이므로, 무한번 미분 가능한 함수만 이 식을 만족한다.
이제 오일러 공식을 유도하는 데 필요한 자연 지수 함수, sin 함수, cos 함수 중 우선 자연 지수 함수를 매클로린 급수 형식으로 전개하고 수렴하는지 확인해본다.
이 매클로린 급수가 수렴하는지 판단하기 위해 비판정법을 진행해본다.
결과가 0이므로 이 급수는 항상 수렴하고, 자연 지수 함수의 매클로린 급수는 유효함을 알 수 있다.
이번에는 sin 함수를 매클로린 급수로 전개해본다.
비판정법을 진행해본다.
이 결과 역시 0이므로 이 급수는 항상 수렴하고, sin 함수의 매클로린 급수도 유효함을 알 수 있다.
이번에는 cos 함수를 매클로린 급수로 전개해본다.
비판정법을 진행해본다.
이 결과 역시 0이므로 이 급수는 항상 수렴하고, cos 함수의 매클로린 급수도 유효함을 알 수 있다.
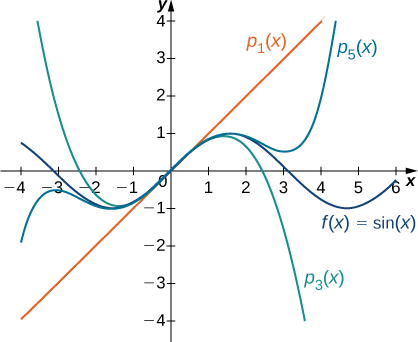
매클로린 급수는 컴퓨터에서 복잡한 함수의 근삿값을 구할 때 유용하게 사용된다.
n개의 항을 가진 급수를 Pn(x)라고 할 때, 급수의 항의 늘어날수록 계산 결과는 sin 함수의 값과 점점 가까워진다.
- 급수항에 계승으로 나눈 상수를 미리 계산해두면, 급수는 덧셈과 곱셈으로만 구성되어 빠르고 효과적으로 함수 값을 구할 수 있다.
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 사원수 대수 (0) | 2023.06.04 |
|---|---|
| 오일러 공식(Euler's formula) (0) | 2023.06.03 |
| 급수(Series) (0) | 2023.06.01 |
| 자연 지수 함수와 삼각함수의 도함수 (0) | 2023.05.31 |
| 도함수(Derivative) (0) | 2023.05.30 |
















