이득우의 게임 수학
사원수(Quarternion)란 4개의 독립된 체계로 구성된 4차원의 수집합으로서, 복소평면을 4차원 공간으로 확장한 개념이다.
복소수와 동일하게 허수를 사용하는 수의 집합으로서, 하나의 실수부와 세 개의 허수부로 구성된다.
사원수를 구성하는 3개의 허수부 i, j, k는 모두 복소수의 허수 단위 i와 같은 성질을 가진다.
세 허수 중 두 허수의 곱은 나머지 하나에 대응되는데, 이들은 회전의 순환 순서 x - y - z - x와 유사하게 i - j - k - i 순서로 대응된다.
ij = k이고 kk = -1이므로, ijk = -1이 성립한다.
- 세 허수의 곱은 -1이 된다.
사원수의 덧셈도 복소수와 유사하게 다음의 성질들을 만족한다.
- 결합법칙
- 교환법칙
- 항등원과 역원이 존재
사원수의 곱셈은 해밀턴 곱(Hamilton product)이라고도 불리며, 모든 요소를 교차해 곱하는 방식이다.
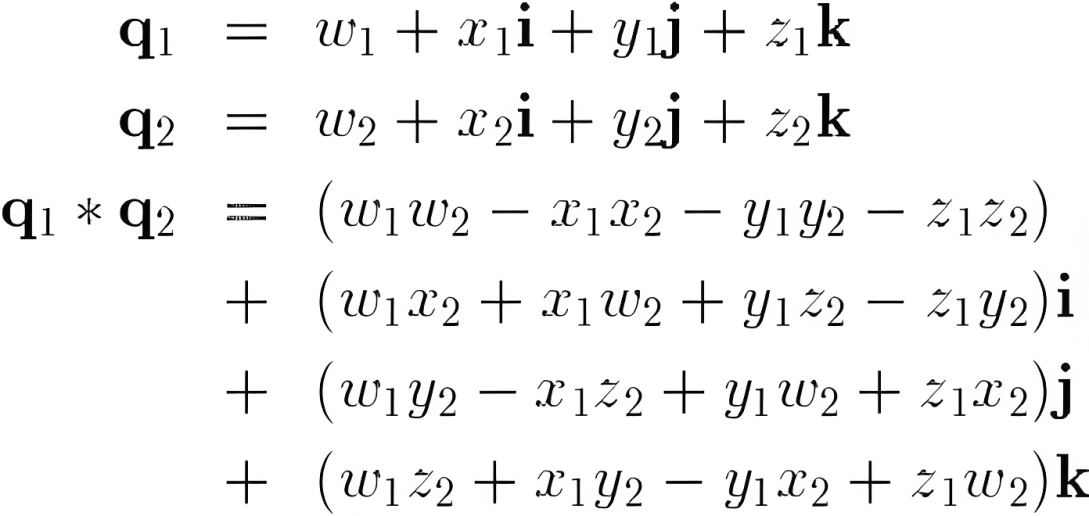
사원수의 곱셈도 복소수와 유사하게 다음의 성질들을 만족한다.
- 결합법칙
- 분배법칙
- 항등원과 역원이 존재
※ 사원수의 곱셈은 복소수의 곱셈과 달리 교환법칙이 성립하지 않기 때문에, 곱셈식을 전개할 때 좌항과 우항이 바뀌지 않도록 주의해야 한다.
사원수의 크기는 복소수와 동일하게 계산하며, 역시 노름(Norm)이라고 부른다.
사원수 중에서 크기가 1인 사원수를 단위 사원수(Unit quaternion)라고 한다.

사원수의 세 허수부의 계수에 음수를 적용한 사원수를 켤레 사원수(Quaternion conjugate)라고 부르며, q*로 표기한다.
사원수와 켤레 사원수의 곱은 복소수 간의 곱의 성질과 동일하다.
임의의 사원수 q에 그 켤레를 곱하면 크기의 제곱이 나온다.
따라서 단위 사원수와 그 켤레 사원수를 곱한 값은 항상 1이 된다.
사원수도 복소수와 동일하게 켤레 사원수의 성질을 이용해 사원수 곱의 역원을 유도할 수 있다.
- 크기가 1인 단위 사원수의 곱셈의 역원은 복소수와 동일하게 켤레 복소수가 됨을 알 수 있다.
4차원 공간은 우리의 인지 범위를 넘어서기 때문에 이를 시각적으로 표현하는 것은 불가능하다.
그래서 사원수를 다룰 때에는, 4차원 공간을 1차원과 3차원으로 분리하고 3차원 공간의 성질을 파악하는 것이 더 효과적이다.
아래와 같이 4개의 축이 모두 직교하는 정팔포체를 4차원 초입방체(Tesseract)라고 한다.

따라서 사원수를 다룰 때에는 허수부를 사용하는 3개의 수 집합을 하나로 묶고, 나머지 실수부는 별도로 관리하는 방법을 사용한다.
세 허수부의 계수를 3차원 벡터 v로 묶는다면, 사원수는 실수와 3차원 벡터 두 가지 요소로 구성된다고 볼 수 있다.
- 이 순서쌍의 원소를 차례대로 실수부(스칼라부), 허수부(벡터부)라고 부른다.
임의의 두 사원수 q₁ = (w₁, v₁), q₂ = (w₂, v₂)의 덧셈과 곱셈을 순서쌍으로 표현해보면 다음과 같다.
사원수의 곱을 순서쌍으로 표현하면 벡터의 내적가 외적을 사용해 깔끔하게 정리된다.
- 사원수의 곱셈에서 교환법칙이 성립하지 않는 이유는 외적이 포함되어 있음을 통해서도 확인할 수 있다.
사원수 중 실수부가 0인 사원수를 특별히 순허수 사원수(Pure imaginary quaternion)라고 한다.
3차원 공간이 사원수를 다루는 4차원 공간의 일부라면, 3차원 공간의 벡터 v(x, y, z)는 순허수 사원수에 대응된다.
임의의 두 사원수 q₁, q₂가 순허수 사원수라고 할 때, 술의 곱셈은 다음과 같이 전개된다.
책의 예제인 CK소프트렌더러에서는 4개의 실수를 사용해 사원수를 다음과 같이 정의하고 있다.
// 책의 예제인 CK소프트렌더러에 정의된 사원수
struct Quaternion
{
public:
...
FORCEINLINE constexpr float RealPart() const { return W; }
FORCEINLINE constexpr Vector3 ImaginaryPart() const { return Vector3(X, Y, Z); }
...
public:
float X = 0.f;
float Y = 0.f;
float Z = 0.f;
float W = 1.f;
};'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 사원수의 회전 (0) | 2023.06.06 |
|---|---|
| 사원수와 오일러 공식 (0) | 2023.06.05 |
| 오일러 공식(Euler's formula) (0) | 2023.06.03 |
| 매클로린 급수(Maclaurin series) (0) | 2023.06.02 |
| 급수(Series) (0) | 2023.06.01 |















