이득우의 게임 수학
회전 사원수 q를 사용해 임의의 회전축 n에 대해 3차원 공간의 벡터 v를 각 θ만큼 회전시키는 방법을 확인해본다.
3차원 공간의 벡터 v(x, y, z)는 순허수 사원수에 대응된다.
회전축 n(a, b, c)은 단위 벡터이기 때문에 a² + b² + c² = 1을 만족하고, 회전축 n을 기준으로 각 θ만큼 회전시키는 회전 사원수 q는 (cosθ, sinθ · n)의 값을 가진다.
회전 사원수 q를 사용해 벡터를 회전시키는 방법은, 회전 사원수를 벡터의 왼쪽에 배치하고 둘을 곱하는 것이다.
- 사원수의 곱셈을 교환법칙이 성립하지 않기 때문에, 항상 곱하는 순서에 주의해야 한다.
그런데 계산 결과를 보면 순허수 사원수가 아닌 네 요소를 모두 사용하는 일반 사원수가 나오기 때문에, 순허수 사원수에 대응했던 3차원 공간의 요소로 사용할 수 없게 된다.
3차원 공간에서 벡터를 회전시키는 용도로 사원수를사용하기 위해서는 사원수 곱의 결과가 항상 순허수 사원수가 되는 특별한 수식을 찾아야 한다.
회전 사원수의 벡터 n은 로드리게스 회전 공식의 축-각 회전에 대응하는 벡터다.
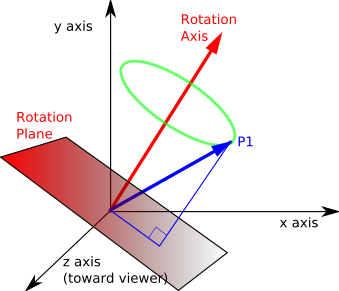
벡터 v를 회전축 n에 평행한(수평인) 성분과 수직인 성분으로 나눠보면 다음과 같다.
벡터 v를 각 θ만큼 회전시킨 벡터를 v'으로 한다.

최종 회전 벡터 v'은 회전축에 수직인 성분만 회전시켜 수평 성분과 더하면 구할 수 있다.

오일러 공식을 활용해 회전 사원수 q를 자연 지수 함수로 바꿔 표현하면 다음과 같다.
우변의 두 번째 항인 회전 사원수와 벡터의 곱셈은 다음과 같이 전개된다.
회전축에 수직인 벡터와 회전 사원수의 곱으로 얻어지는 사원수는 실수부가 항상 1인 순허수 사원수가 되므로, 3차원 공간의 벡터에 대응할 수 있음을 확인했다.
이번에는 연산 순서를 바꿔본다.
- 외적의 성질에 의해 sin 함수의 부호가 반대가 된다.
θ 대신 -θ를 대입하면 다음과 같다.
따라서 두 항의 순서를 바꿔 연산환 결과는 처음 식과 동일하므로, 회전축과 직교하는 벡터에 대해서는 다음 식이 성립한다.
수식에는 등장하지 않지만 회전 사원수와 회전축에 평행한 벡터의 사원수 곱이 가지는 성질을 살펴본다.
- 평행인 두 벡터의 외적은 영벡터가 되므로, 이번에는 실수부가 남고 허수부가 단순화된다.
사원수의 곱셈에서 교환법칙의 성립을 방해하던 외적 부분이 사라졌기 때문에, 평행인 벡터와의 곱은 항상 교환법칙이 성립한다.
각 θ의 회전을 수행하는 회전 사원수는 이를 절반으로 나눈 각의 회전 사원수를 두 번 곱한 결과와 동일하다.
회전 사원수와 그 켤레 사원수의 곱은 마우런 변환 없는 0° 회전을 만들어내므로, 이들의 곱은 곱셈의 항등원 1에 대응된다.
직교하는 벡터와 평행하는 벡터의 성질을 활용해 3차원 공간에서의 회전을 전개하면 다음과 같이 정리된다.
이제 간략해진 최종 식에서 자연 지수 함수를 다시 사원수 형태로 바꿔본다.
- 각 θ가 아닌, θ/2만큼 돌리는 회전을 회전 사원수 q로 표현한다.
- 반대 방향으로 θ/2만큼 돌리는 회전 사원수는 켤레 사원수 q*이 된다.
회전 사원수 q의 값은 다음과 같다.
이제 절반의 각만 회전시키는 단위 사원수를 곱했을 때, 그 결과가 항상 실수부가 0인 순허수 사원수가 나오는지 확인해보면 된다.
회전 사원수 q의 실수부와 허수부를 w와 r로 표시하면 다음과 같다.
사원수 형태로 나타낸 v'의 식을 내적과 외적으로 나타내 전개하면 다음과 같은 결과가 나온다.
2(r x v)를 t로 치환하면 최종적으로 벡터 v'은 다음과 같이 정리된다.
이로써 사원수를 사용해 3차원 공간의 벡터 v를 임의의 회전축 n을 중심으로 각 θ만큼 회전시키는 수식이 완성됐다.
3차원 공간의 임의의 회전축 n과 회전할 각 θ가 주어졌다면, θ의 절반을 사용해 사원수를 만들어 이를 계산한다.
책의 예제인 CK소프트렌더러에서 3차원 공간에서 임의의 회전축 n에 대해 θ만큼 주어진 벡터 v를 회전하는 함수는 다음과 같다.
// 책의 예제인 CK소프트렌더러에서 회전 사원수를 이용해 3차원 공간의 벡터를 회전하는 함수
FORCEINLINE constexpr Vector3 Quaternion::RotateVector(const Vector3& InVector) const
{
// 회전 사원수의 허수부 벡터
Vector3 r(X, Y, Z);
Vector3 t = r.Cross(InVector) * 2.f;
// W는 회전 사원수의 실수부 값
return InVector + (t * W) + r.Cross(t);
}
한 가지 흥미로운 사실은 v'의 최종 계산 식을 θ/2가 아닌 θ를 중심으로 전개하면 로드리게스 회전 공식이 유도된다는 점이다.
이로써, 회전 사원수의 허수부 벡터에서 설정한 벡터 n은 축-각 회전에서 회전축의 기능을 수행한다는 사실을 확인했다.
이번에는 같은 회전축에 두 개의 가른 각 2α, 2β를 연속해서 회전시키는 경우를 알아본다.
첫 번째 회전을 적용한 벡터를 v', 두 번쨰 회전을 적용한 벡터를 v''으로 표기하면 다음과 같다.
v''을 계산하면 다음과 같이 전개된다.
이로써, 서로 다른 두 회전 사원수의 곱은 두 각을 합한 회전 사원수와 형태가 동일하다는 점도 확인했다.
아래는 사원수 구조체에서 회전을 수행하기 위해 제공하는 곱셈 연산자의 로직이다.
- 회전 사원수와 회전 사원수의 곱은 두 각을 합한 사원수에 대응된다.
- 사원수와 3차원 벡터의 곱은 사원수로 표현되는 회전축과 각으로 벡터를 회전한 결과에 대응된다.
// 책의 예제인 CK소프트렌더러에 정의된 사원수
struct Quaternion
{
public:
....
// 사원수와 사원수의 곱셈 연산
FORCEINLINE constexpr Quaternion operator*(const Quaternion& InQuaternion) const
{
Quaternion result;
Vector3 v1(X, Y, Z), v2(InQuaternion.X, InQuaternion.Y, InQuaternion.Z);
result.W = W * InQuaternion.W - v1.Dot(v2);
Vector3 v = v2 * W + v1 * InQuaternion.W + v1.Cross(v2);
result.X = v.X;
result.Y = v.Y;
result.Z = v.Z;
return result;
}
// 사원수와 벡터의 곱셈 연산
FORCEINLINE constexpr Vector3 operator*(const Vector3& InVector) const
{
return RotateVector(InVector);
}
...
};'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 사원수의 보간 (0) | 2023.06.08 |
|---|---|
| 사원수의 변환 (0) | 2023.06.07 |
| 사원수와 오일러 공식 (0) | 2023.06.05 |
| 사원수 대수 (0) | 2023.06.04 |
| 오일러 공식(Euler's formula) (0) | 2023.06.03 |






















