이득우의 게임 수학
사원수는 로드리게스 회전과 동일한 축-각 방식을 사용해 3차원 공간의 회전을 표현한다.
사원수를 사용하는 경우의 장점은 다음과 같다.
1. 오일러 각과 쉽게 변환이 가능하며, 회전 행렬 제작이 용이하다.
2. 행렬과 상호 변환이 가능하다.
3. 임의의 축에 대한 회전 표현이 가능하기 때문에 짐벌락 현상을 방지할 수 있다.
4. 임의의 축에 대한 회전 보간 값을 구할 수 있다.
5. 4개의 숫자로 표현하기 때문에 저장 공간을 효율적으로 쓸 수 있다.
회전 방식별 장단점은 다음과 같다.
| 오일러 각 | 행렬 | 사원수 | |
| 저장 공간 | 3 | 9 | 4 |
| 짐벌락 현상 없음 | X | O | O |
| 회전 보간 | 한 기저 축에 대해서만 가능 | X | 임의의 축에 가능 |
| 직관성 | O | X | X |
다른 회전 방식에 비해 사원수의 장점은 회전 보간이 가능하다는 것이다.
사원수를 4차원 공간의 벡터로 생각하고, 두 사원수가 만들어내는 4차원 공간에서의 평면을 상상해본다.
해당 평면에서 주어진 비율 t에 대응하는 사원수는 두 사원수의 위치를 선형 보간한 지점이 된다.
주어진 비율 t에 대응하는 중간 사원수를 구하는 식은 다음과 같다.
- 선형 보간으로 얻어지는 사원수는 크기가 1인 단위 사원수가 아니기 때문에, 회전 사원수로 만들기 위해서는 정규화 과정을 거쳐야 한다.
선형 보간법은 빠르고 간편하게 사용할 수 있지만, 아래 그림처럼 원의 궤적을 따라 발생한 회전을 정확히 반영하지는 못한다.
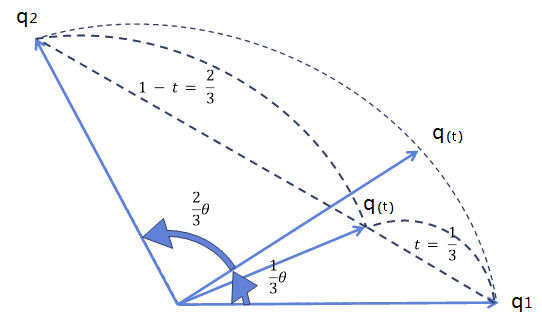
좀 더 높은 수준의 결과물을 위해 회전의 움직임을 따르는 중간 사원수를 구하려면 두 사원수가 이루는 각을 θ로 지정하고, 주어진 비율 t를 사용해 두 각을 tθ와 (1 - t)θ로 나눠야 한다.
- (1 - t)θ = α, tθ = β로 치환한다.
첫 번째 사원수를 x축에 일치시키고 이 벡터를 x, x에 직교하는 벡터를 y, 두 번째 사원수에 해당하는 벡터를 u라고 할 때, 중간 사원수 v는 다음과 같다.
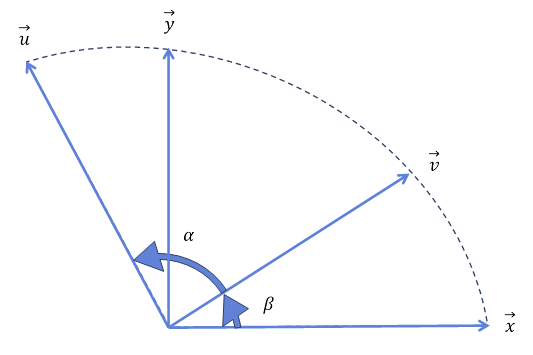
두 사원수가 만드는 각을 θ라고 했을 때, 벡터 v는 서로 직교하는 두 기저 벡터 x와 y의 조합으로 계산된다.
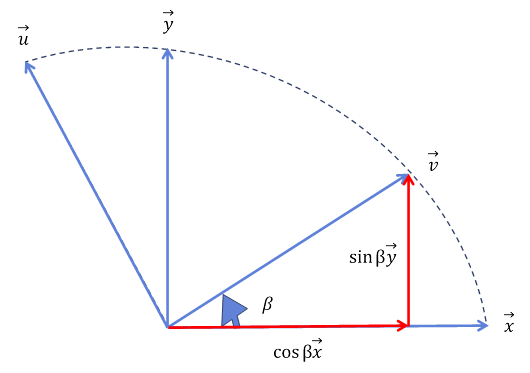
그런데 벡터 x에 직교하는 벡터 y 값을 모르므로, 벡터 u와 삼각함수를 활용해 이를 구해야 한다.

이 값을 벡터 v의 식에 대입하면 최종 벡터를 구하는 식은 다음과 같다.
따라서, 원의 궤적을 따라 발생한 회전을 보간하는 데 필요한 계수 α, β는 다음과 같다.
이 계수를 q'에 대입하면 최종 구면 선형 보간(Slerp, Spherical linear interpolation) 식이 만들어진다.
사원수의 구면 선형 보간을 구현하는 데 필요한 두 계수의 식 외에 고려할 점이 몇 가지 있다.
- 긴 경로와 짧은 경로 중 선택
- 두 사원수가 평행해 sinθ가 0인 경우
먼저, 두 사원수로부터 나오는 회전 경로는 항상 긴 경로와 짧은 경로가 있는데 이 중 하나를 선택해야 한다는 것이다.

따라서 언제나 짧은 경로를 선택하고자 한다면, 보간을 진행하기 전에 두 벡터의 사잇각이 180°보다 작은지 확인해야 한다.
- 180°보다 크다면, 짧은 경로의 결과가 나오도록 계산 방법을 조정해야 한다.
그런데 여기서, 우리가 사용하는 사원수에는 항상 회전시키고자 하는 각의 절반이 저장되어 있기 때문에 이를 감안해야 한다.
예를 들어 사원수 (0, (1, 0, 0))을 4차원 공간의 회전에 사용한다면, 이는 x축 90° 회전이 된다.
하지만, 이를 3차원 공간의 회전에 사용한다면 x축 180° 회전으로 해석된다.
따라서 어떤 사원수에 저장된 각이 θ°라면, 해당 사원수를 통해 구현된 3차원 공간의 회전은 그 2배인 2θ°가 된다.
그렇기 때문에 긴 경로를 탐지하는 사잇각 조건은 180°가 아닌 90°가 되어야 하며, 이는 내적을 사용해 판별이 가능하다.
q1 · q2 < 0이라면, 사잇각이 90°보다 크므로 3차원 공간에서 180°보다 큰 긴 경로의 회전에 사원수가 사용되고 있다는 의미이다.
- 두 번째 사원수를 짧은 경로의 사원수로 바꿔주어야 한다.
짧은 경로의 사원수는 해당 사원수를 반전시키는 것으로 간단하게 처리할 수 있다.
- 구현 로직에서 내적 값도 함께 반전시켜주어야 한다.
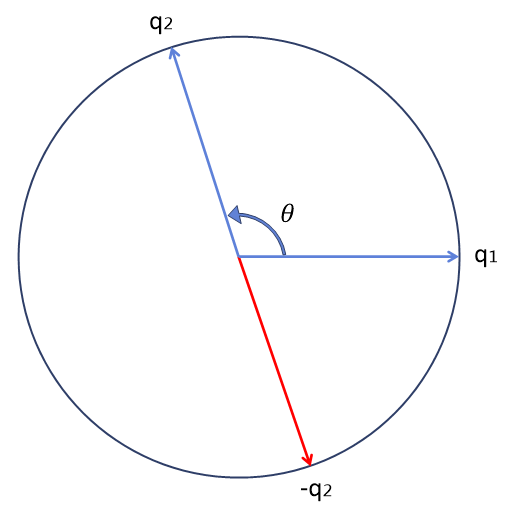
두 번째 고려할 점은 두 사원수의 방향이 평행해 sinθ가 0이 되어 구면 선형 보간 식의 계산이 불가능한 경우이다.
- 역시 내적을 통해 판별할 수 있다.
그러므로 내적의 크기가 1이거나 1에 매우 근접해 두 사원수의 사잇각이 매우 작은 상황이라면, 일반 선형 보간을 사용하도록 한다.
책의 예제인 CK소프트렌더러에 구현된 구면 선형 보간 로직은 다음과 같다.
- 책에서는 항상 짧은 거리의 각으로만 보간하도록 구현했지만, 조금 수정하면 긴 거리의 각으로 회전하는 로직으로 바꿀 수도 있다.
// 책의 예제인 CK소프트렌더러에 구현된 구면 선형 보간
FORCEINLINE Quaternion Quaternion::Slerp(const Quaternion & InQuaternion1, const Quaternion & InQuaternion2, float InRatio)
{
Quaternion q1 = InQuaternion1, q2 = InQuaternion2;
// 사원수의 내적 구하기
float dot = q1.X * q2.X + q1.Y * q2.Y + q1.Z * q2.Z + q1.W * q2.W;
// 내적 값이 0보다 작으면 최단거리를 사용하도록 방향을 전환
if (dot < 0.0f) {
q1 = -q1;
dot = -dot;
}
float alpha = 1.f, beta = 0.f;
// 두 사원수의 사잇각이 작으면 선형 보간으로 수행
if (dot > 0.9995f)
{
alpha = 1.0f - InRatio;
beta = InRatio;
}
else
{
const float theta = acosf(dot);
const float invSin = 1.f / sinf(theta);
alpha = sinf((1.f - InRatio) * theta) * invSin;
beta = sinf(InRatio * theta) * invSin;
}
Quaternion result;
result.X = alpha * q1.X + beta * q2.X;
result.Y = alpha * q1.Y + beta * q2.Y;
result.Z = alpha * q1.Z + beta * q2.Z;
result.W = alpha * q1.W + beta * q2.W;
return result;
}
구면 선형 보간은 카메라 움직임이나 캐릭터 애니메이션과 같이, 시간에 따른 부드러운 회전을 구현하는 데 유용하게 사용된다.


3차원 공간에서 멈춰있는 물체의 회전을 설정하고 회전에 관련된 정보를 보여줄 때는 오일러 각 방식이 편리하지만, 시간에 따라 변화는 회전을 처리할 때는 짐벌락 현상이 없는 사원수를 사용하는 것이 안전하고 간편한다.
따라서 3차원 트랜스폼을 안정적으로 구동시키기 위해서는 사원수를 기반으로 하고, 회전을 지정하거나 게임 로직에서 직관적으로 사용할 수 있는 오일러 각 방식과 자유롭게 변환할 수 있는 기능을 제공해야 한다.
또한, 렌더링 로직에서 필요한 회전 변환 행렬을 사원수로부터 만드는 기능도 제공해야 한다.
책의 예제인 CK소프트렌더러에서 사원수를 기반으로 한 트랜스폼 시스템은 다음과 같다.
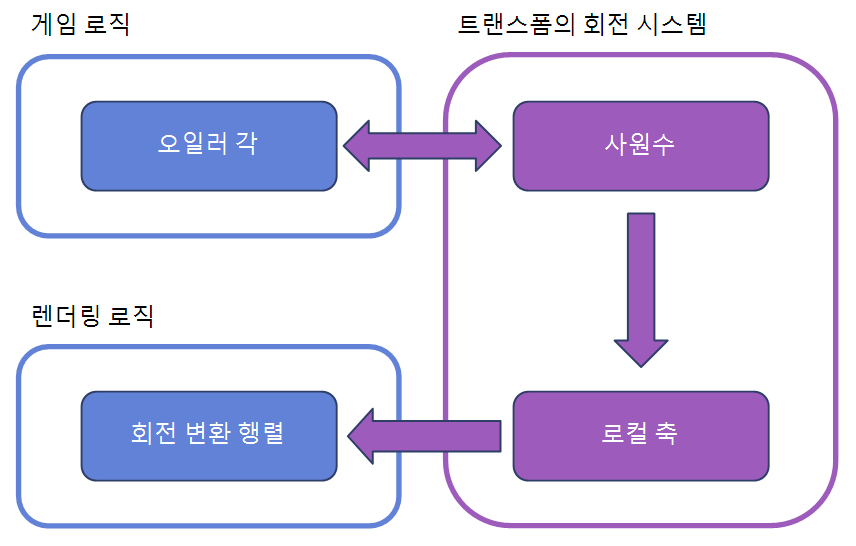
// 책의 예제인 CK소프트렌더러에 정의된 사원수 기반의 트랜스폼
class TransformComponent
{
...
void AddYawRotation(float InDegree)
{
// 사원수를 오일러 각으로 변환
Rotator r = _Rotation.ToRotator();
r.Yaw += InDegree;
r.Clamp();
// 오일러 각을 다시 사원수로 변환
_Rotation = Quaternion(r);
}
...
constexpr void SetRotation(const Rotator& InRotator) { _Rotation = Quaternion(InRotator); }
void SetRotation(const Matrix3x3& InMatrix) { _Rotation = Quaternion(InMatrix); }
constexpr void SetRotation(const Quaternion& InQuaternion) { _Rotation = InQuaternion; }
...
FORCEINLINE constexpr Vector3 GetPosition() const { return _Position; }
FORCEINLINE constexpr Quaternion GetRotation() const { return _Rotation; }
FORCEINLINE constexpr Vector3 GetScale() const { return _Scale; }
FORCEINLINE constexpr Vector3 GetLocalX() const { return _Rotation * Vector3::UnitX; }
FORCEINLINE constexpr Vector3 GetLocalY() const { return _Rotation * Vector3::UnitY; }
FORCEINLINE constexpr Vector3 GetLocalZ() const { return _Rotation * Vector3::UnitZ; }
FORCEINLINE Matrix4x4 GetModelingMatrix() const;
{
return Matrix4x4(
Vector4(GetLocalX() * _Scale.X, false),
Vector4(GetLocalY() * _Scale.Y, false),
Vector4(GetLocalZ() * _Scale.Z, false),
Vector4(_Position, true)
);
}
private:
Vector3 _Position = Vector3::Zero;
Quaternion _Rotation;
Vector3 _Scale = Vector3::One;
};'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 트랜스폼 계층 구조 (0) | 2023.06.10 |
|---|---|
| 스켈레탈 애니메이션 (0) | 2023.06.09 |
| 사원수의 변환 (0) | 2023.06.07 |
| 사원수의 회전 (0) | 2023.06.06 |
| 사원수와 오일러 공식 (0) | 2023.06.05 |













