이득우의 게임 수학
이번에는 캐릭터를 제작하기 위한 트랜스폼의 계층 구조에 대해 알아본다.
실습해 본 예제에서는 Left와 Right 본이 서로 연결되지 않고 독립적으로 움직였지만, 일반적으로 캐릭터를 구성하는 본은 모두 유기적으로 연결되어 있으며, 부모-자식 관계의 계층 구조가 형성되어 있다.
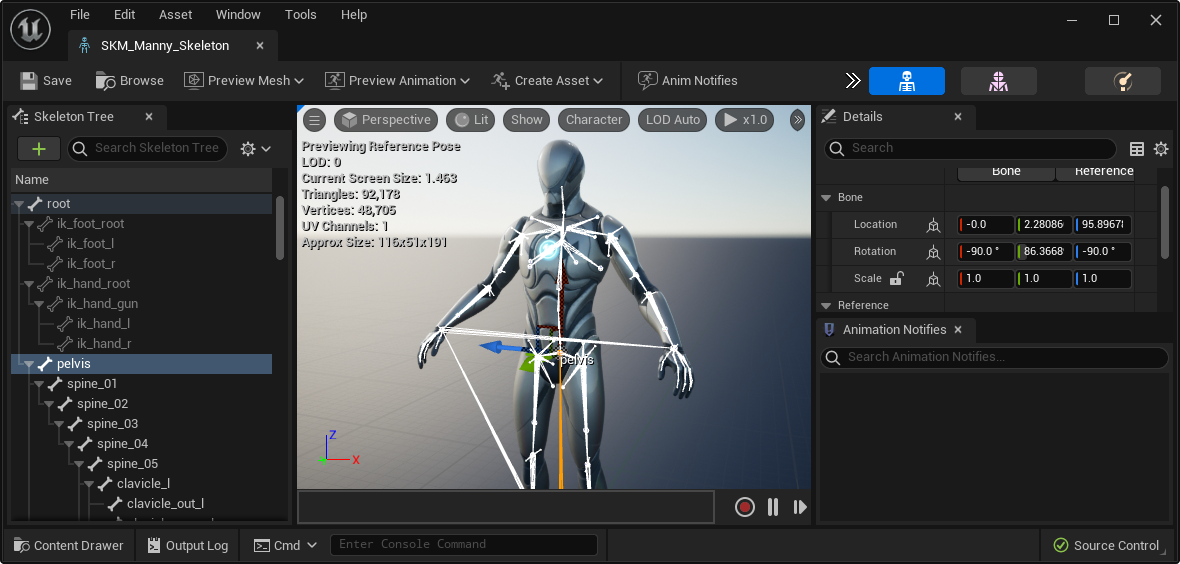
손가락이 움직이지 않아도 팔목이 움직이면 손가락의 최종 위치가 달라지듯이, 게임 캐릭터도 부모-자식의 계층 구조를 가져야 사람의 움직임을 구현할 수 있다.
부모-자식 계층 관계에서 부모와 자식 트랜스폼이 가져야 하는 규칙을 정리하면 다음과 같다.
- 부모가 움직이면 그만큼 자식도 움직이지만, 자식의 움직임에 부모는 영향을 받지 않는다.
- 부모는 여러 자식을 가질 수 있지만, 자식은 하나의 부모만 갖는다.
계층 구조에서 부모가 없는 최상단 트랜스폼을 루트(Root) 트랜스폼이라고 한다.
책의 예제인 CK소프트렌더러에서 계층 구조를 지원하도록 기능을 확장한 트랜스폼은 다음과 같다.
// 책의 예제인 CK소프트렌더러에서 트랜스폼의 계층 관계를 지원하기 위해 추가된 부분
class TransformComponent
{
...
public: // 계층 구조 관련 함수
bool SetRoot();
TransformComponent& GetRoot();
bool SetParent(TransformComponent& InTransform);
FORCEINLINE bool HasParent() const { return _ParentPtr != nullptr; }
vector<TransformComponent*>& GetChildren() { return _ChildrenPtr; }
vector<TransformComponent*>::const_iterator ChildBegin() const { return _ChildrenPtr.begin(); }
vector<TransformComponent*>::const_iterator ChildEnd() const { return _ChildrenPtr.end(); }
...
private: // 계층 구조를 위한 변수
...
TransformComponent* _ParentPtr = nullptr;
vector<TransformComponent*> _ChildrenPtr;
};
트랜스폼 데이터는 부모로부터 상대적인 로컬 트랜스폼(Local transform)과 자신이 속한 공간에서 절대적인 월드 트랜스폼(World transform)으로 분리해 관리하는 것이 효과적이다.
- 로컬 트랜스폼은 상대 트랜스폼(Relative transform), 월드 트랜스폼은 절대 트랜스폼(Absolute transform)이라고도 한다.
트랜스폼을 두 가지로 분리해 관리하는 이유는, 계층 구조가 변동되는 다양한 상황에 효과적으로 대처할 수 있기 때문이다.
// 책의 예제인 CK소프트렌더러에서 트랜스폼 정보를 이원화하여 제공하는 부분
class TransformComponent
{
...
public: // 로컬 트랜스폼 관련 함수
FORCEINLINE Transform& GetLocalTransform() { return _LocalTransform; }
FORCEINLINE void SetLocalTransform(const Transform& InTransform) { _LocalTransform = InTransform; UpdateWorld(); }
...
public: // 월드 트랜스폼 관련 함수
FORCEINLINE Transform& GetWorldTransform() { return _WorldTransform; }
FORCEINLINE void SetWorldTransform(const Transform& InTransform) { _WorldTransform = InTransform; UpdateLocal(); }
...
private: // 계층 구조를 위한 변수
Transform _LocalTransform;
Transform _WorldTransform;
...
};
월드와 로컬 트랜스폼 값이 서로 일관되게 하기 위해 고려해야 할 점들은 다음과 같다.
부모의 월드 트랜스폼이 변경된 경우,
후손들의 로컬 트랜스폼은 변하지 않으나, 월드 트랜스폼은 갱신되어야 한다.
나의 로컬 트랜스폼이 변경된 경우,
후손들의 로컬 트랜스폼은 변하지 않으나, 나와 후손들의 월드 트랜스폼은 갱신되어야 한다.
나의 월드 트랜스폼이 변경된 경우,
후손들의 로컬 트랜스폼은 변하지 않으나, 나의 로컬 트랜스폼과 후손들의 월드 트랜스폼은 갱신되어야 한다.
새로운 부모로 편입하는 경우,
(부모-자식 관계를 다시 설정하고 트랜스폼 정보를 갱신할 뿐, 위치를 이동시키는 작업이 아니다.)
우선, 나를 부모로부터 독립시키고 최상단의 루트 트랜스폼으로 만들어준다.
(임시로 루트로 만든 것일 뿐이므로, 기존 루트의 로컬 트랜스폼을 갱신하지는 않는다.)
루트 트랜스폼은 로컬과 월드가 같은 값을 가지므로, 나의 로컬 트랜스폼에 월드 트랜스폼을 덮어쓴다.
(나의 월드 트랜스폼은 변경되지 않았으므로, 후손들의 월드 트랜스폼은 갱신할 필요가 없다.)
나를 새로운 부모의 자식으로 등록하고, 나의 로컬 트랜스폼을 갱신한다.
위와 같은 계층 구조에 관한 문제를 구현하기 위해서는 다음의 두 가지 기능이 필요하다.
- 부모의 월드 트랜스폼과 나의 로컬 트랜스폼을 비교해, 나의 월드 트랜스폼을 계산하는 기능
- 부모의 월드 트랜스폼과 나의 월드 트랜스폼을 비교해, 나의 로컬 트랜스폼을 계산하는 기능
이 기능을 구현할 때는 트랜스폼의 세 요소인 크기, 회전, 이동에 대해 생각해봐야 한다.
우선 나의 월드 트랜스폼을 계산하는 기능부터 살펴본다.
내 월드 트랜스폼의 크기 s.world는 부모 월드 트랜스폼의 크기 sᴾ와 내 로컬 트랜스폼의 크기 s를 곱한 값이 된다.
- 크기를 구성하는 세 축은 모두 직교하므로, 각 축의 크기는 독립적으로 적용된다.
임의의 두 벡터의 각 요소들을 곱하는 연산을 기호 *로 나타내면, 내 월드 크기는 다음과 같이 정리할 수 있다.
이번에는 크기를 배제한 상태에서 회전이 어떻게 진행되는지 생각해본다.
부모의 월드 회전을 사원수 qᴾ가 담당하고, 나의 로컬 회전을 사원수 q가 담당한다고 하면 나의 월드 회전은 다음과 같다.
마지막으로 이동해 대해 생각해본다.
부모 월드 트랜스폼의 세 로컬 축을 각각 xᴾ, yᴾ, zᴾ로 설정하고 이동 값을 벡터 tᴾ로 설정하면, 부모 월드 트랜스폼으로부터의 모델링 행렬 Mᴾ.world는 다음과 같다.
마찬가지로, 내 로컬 트랜스폼의 세 로컬 축을 각각 x, y, z로 설정하고 이동 값을 벡터 t로 설정하면, 부모 로컬 트랜스폼으로부터의 모델링 행렬 M.local은 다음과 같다.
그렇다면 ,내 월드 트랜스폼의 행렬 M.world는 다음과 같이 행렬 곱으로 계산된다.
여기서 구한 M.world의 마지막 4열 값이 월드 트랜스폼의 이동 값이 될 것이다.
- 따라서, 모두 계산하지 않고 4열에 대한 값만 계산하면 다음과 같다.
책의 예제인 CK소프트렌더러에서 계산한 값들을 이용해 나의 최종 월드 트랜스폼을 구하는 부분은 다음과 같다.
// 책의 예제인 CK소프트렌더러에서 로컬 트랜스폼을 월드 트랜스폼으로 변환하는 함수
FORCEINLINE constexpr Transform Transform::LocalToWorld(const Transform& InParentWorldTransform) const
{
// 현재 트랜스폼 정보가 로컬인 경우
Transform result;
result.SetScale(InParentWorldTransform.GetScale() * GetScale());
result.SetRotation(InParentWorldTransform.GetRotation() * GetRotation());
result.SetPosition(InParentWorldTransform.GetPosition() + InParentWorldTransform.GetRotation() * (InParentWorldTransform.GetScale() * GetPosition()));
return result;
}
이번에는 월드 트랜스폼으로부터 로컬 트랜스폼을 계산하는 기능을 구현해본다.
이를 위해서는 부모의 월드 트랜스폼과 나의 월드 트랜스폼의 차이를 계산해야 하는데, 이는 월드 공간을 카메라 중심의 뷰 공간으로 바꾸는 작업과 유사하다.
- 부모의 월드 트랜스폼을 중심으로 나의 월드 트랜스폼을 해석할 수 있다면, 그 값이 나의 로컬 트랜스폼이 될 것이다.
카메라 트랜스폼에 역변환을 적용한 것처럼, 부모의 월드 트랜스폼에 역변환을 반영하면 된다.
크기의 역변환에 대해 먼저 생각해보면, 크기의 역변환은 크기의 역수로 계산된다.
그리고 크기를 배제한 트랜스폼의 회전을 시원수 q로 지정한다면, 회전의 역변환은 켤레 사원수 q*가 된다.
마지막으로 이동 값 t의 역변환을 구하기 위해서는 트랜스폼을 담당하는 모델링 행렬 M = TRS의 역행렬을 직접 계산해야 한다.
모델링 행렬 M의 역행렬에서 위치에 대한 4열의 값은 다음과 같다.
책의 예제인 CK소프트렌더러에서 계산한 값들을 이용해 주어진 트랜스폼의 역변환을 구하는 부분은 다음과 같다.
// 책의 예제인 CK소프트렌더러에서 주어진 트랜스폼의 역변환을 구하는 함수
FORCEINLINE constexpr Transform Transform::Inverse() const
{
// 로컬 정보만 남기기 위한 트랜스폼 ( 역행렬 )
Vector3 reciprocalScale = Vector3::Zero;
if (!Math::EqualsInTolerance(Scale.X, 0.f)) reciprocalScale.X = 1.f / Scale.X;
if (!Math::EqualsInTolerance(Scale.Y, 0.f)) reciprocalScale.Y = 1.f / Scale.Y;
if (!Math::EqualsInTolerance(Scale.Z, 0.f)) reciprocalScale.Z = 1.f / Scale.Z;
Transform result;
result.SetScale(reciprocalScale);
result.SetRotation(Rotation.Inverse());
result.SetPosition(result.GetScale() * (result.GetRotation() * -Position));
return result;
}
역변환 기능을 사용해 부모의 월드 트랜스폼의 역변환을 구한 후, 나의 월드 트랜스폼에 곱하면 나의 로컬 트랜스폼을 만들 수 있다.
부모 트랜스폼이 역변환된 행렬도 트랜스폼의 일종이므로, 동일한 방식으로 역변환된 트랜스폼의 각 요소를 계산하면 된다.
책의 예제인 CK소프트렌더러에서 위 수식들을 사용해 부모의 월드 트랜스폼을 기준으로 나의 로컬 트랜스폼을 구하는 함수는 다음과 같다.
FORCEINLINE constexpr Transform Transform::WorldToLocal(const Transform& InParentWorldTransform) const
{
// 현재 트랜스폼 정보가 월드인 경우
Transform invParent = InParentWorldTransform.Inverse();
Transform result;
result.SetScale(invParent.GetScale() * GetScale());
result.SetRotation(invParent.GetRotation() * GetRotation());
result.SetPosition(invParent.GetPosition() + (invParent.GetRotation() * (invParent.GetScale() * GetPosition())));
return result;
}'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 완독 및 후기 (0) | 2023.06.12 |
|---|---|
| 캐릭터 메시와 애니메이션 (0) | 2023.06.11 |
| 스켈레탈 애니메이션 (0) | 2023.06.09 |
| 사원수의 보간 (0) | 2023.06.08 |
| 사원수의 변환 (0) | 2023.06.07 |
















