이득우의 게임 수학
미분은 미분 가능한 함수를 대상으로 특정 지점에서의 접선의 기울기를 구하는 작업이다.
- 자연 지수 함수, sin 함수, cos 함수는 모두 미분 가능한 함수이다.
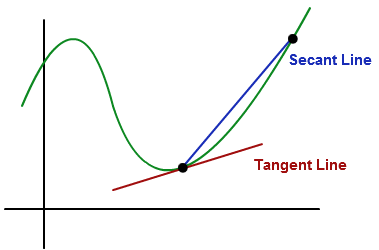
다음과 같이 미분 가능한 함수가 주어졌을 때, 함수 위의 임의의 두 점을 연결해 만든 직선을 할선(Secant line)이라고 한다.

임의의 두 점의 x값이 a, b라고 할 때, 할선의 기울기는 m은 다음과 같다.

a를 고정시킨 상태에서 b를 서서히 a오 이동시키면 할선의 기울기는 시시각각 변화할 것이다.

b가 a에 도달하면 분모가 0이 되므로 할선이 더 이상 존재하지 않게 되지만, a가 아닌 a에 한없이 가까운 값에 접근했다면 마치 a 지점에서의 기울기처럼 보일 것이다.
- 이렇게 한없이 가까워지는 개념을 이용햐 특정 지점에서의 기울기를 타나내는 선을 접선(Tangent line)이라고 한다.

접선의 기울기 m은 극한을 적용해 다음과 같이 계산한다.

아주 작은 값 h = b - a로 치환하면 다음과 같이 표현할수 있고, 이 때의 m 값은 a에서의 미분 계수(Differential coefficient) 혹은 접선의 기울기라고 한다.

'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 자연 지수 함수와 삼각함수의 도함수 (0) | 2023.05.31 |
|---|---|
| 도함수(Derivative) (0) | 2023.05.30 |
| 자연 지수 함수 (0) | 2023.05.28 |
| 복소평면(Complex plane) (0) | 2023.05.26 |
| 복소수(Complex number) (0) | 2023.05.25 |