이득우의 게임 수학
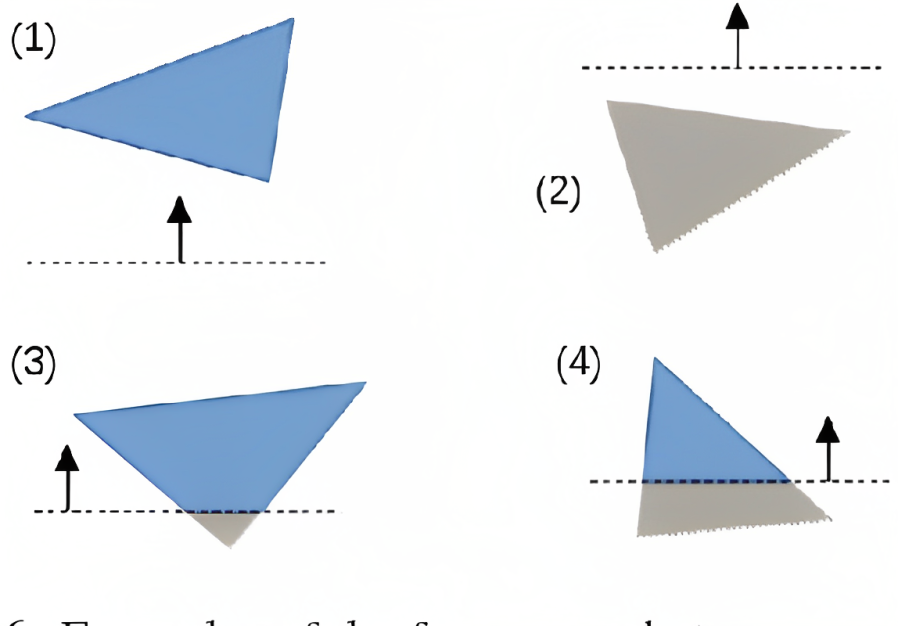
현재 절두체 컬링 구현에서는 카메라를 좌우로 많이 움직일 경우, 공포 영화의 한 장면처럼 아래와 같이 심각한 깨짐 현상이 발생한다.
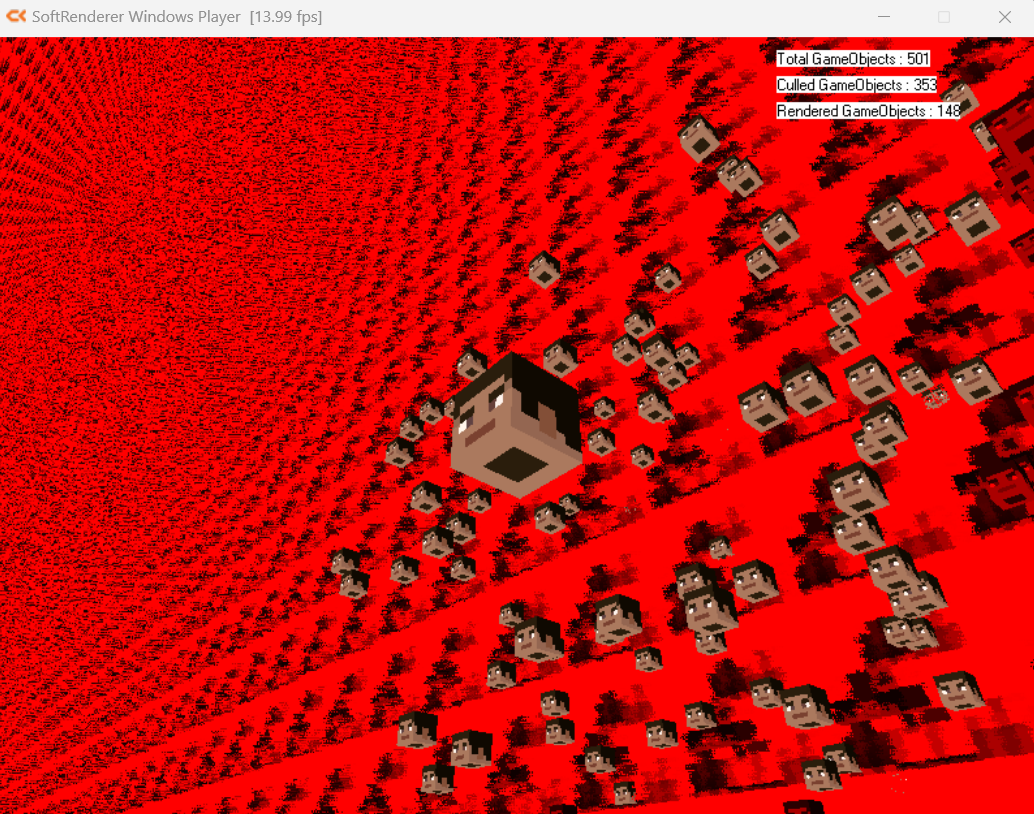
문제의 원인을 알아보기 위해 아래와 같이, 삼각형 CBA 중 점 C가 카메라의 뒤쪽에 있는 경우를 가정해본다.

이를 투영하면 카메라 뒤쪽에 위치한 점 C는 원점을 중심으로 뒤집혀 투영 평면에 투영된다.
- 따라서 위 실행 화면처럼 엉뚱한 삼각형이 그려져 문제가 발생하는 것이다.
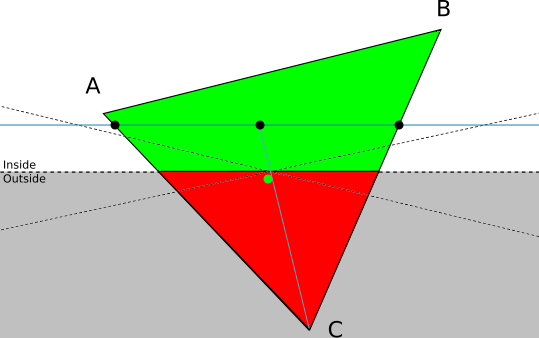
따라서 평면이 올바르게 보이려면 카메마 뒤쪽에 있는 점을 파악해 점이 거꾸로 투영되지 않도록 해야 한다.
원근 투영 행렬에 곱해 생성된 클립 좌표계의 w값은 뷰 공간에서의 깊이를 의미한다.
- 0 < w
카메라 앞에 점이 있다. - w < 0
카메라 뒤에 점이 있다. - w = 0
카메라 초점에 점이 있다.
w가 음수인 카메라 뒤쪽의 점을 파악해 이들이 엉뚱하게 투영되지 않도록 삼각형을 잘라내는 작업을 삼각형 클리핑이라고 한다.
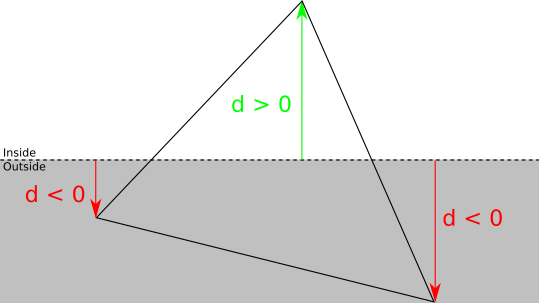
삼각형 클리핑은 월드 공간의 좌표를 사용하지 않고 투영 행렬을 적용한 사영 공간에서 진행된다.
- 사영 공간에서 진행하는 것이 더 쉽기 때문이고, 이것이 사영 공간의 좌표를 클립 좌표라고 부르는 이유이다.
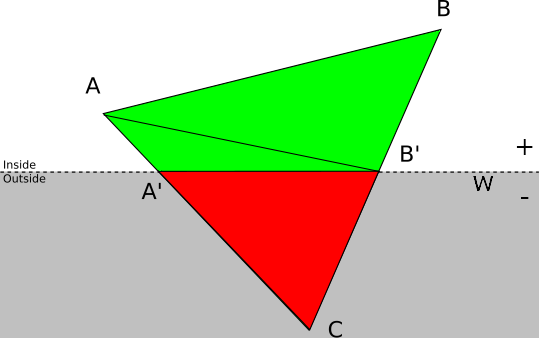
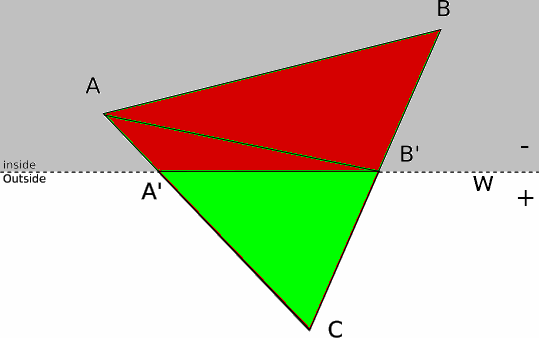
아래의 상황에서는 w가 음수인 점 C로 인해 붉은색 영역을 잘라내야 하고, 그러기 위해서는 점 C를 w = 0 평면에 투영한 두 점 A', B'의 좌표를 구해야 한다.

점 B'을 살펴보면 선분 CB 위의 점이다.
따라서, 점 B'의 좌표는 아핀 결합의 직선의 방정식을 활용해 다음과 같이 구할 수 있다.
점 B'은 w = 0인 직선에 위치하므로 점 B'의 w값은 0이다.
각 점의 w값으로 나타내면 다음과 같다.
t₁에 대해 정리하면 다음과 같고, 점 A'의 좌표를 구하기 위한 t₂의 값도 같은 방법으로 구할 수 있다.
이제 t₁, t₂를 대입해 점 A', B'의 좌표를 구할 수 있지만, 잘라내고 남은 영역이 삼각형이 아닌 사각형을 이룬다는 문제가 있다.

우리는 그릴 때 항상 삼각형을 사용하므로, 사각형을 두 개의 삼각형으로 분할해야 한다.
- 분할할 때는 면의 방향이 동일하도록 정점의 순서가 자르기 전의 삼각형 순서와 동일해야 한다.
자르기 전의 정점 배치 순서가 △CBA였다면, 두 삼각형의 정점 순서는 다음과 같다.
- △B'BA
- △B'AA'
한 점이 카메라 뒤쪽에 있는 상황과 달리, 두 점이 카메라 뒤에 있는 상황도 있을 수 있다.
- 이때는 빨간 영역을 잘라내고 남은 영역은 언제나 삼각형이 만들어지므로, 점 A'과 B'의 좌표만 구해도 된다.
삼각형의 세 점이 모두 카메라 뒤쪽(w < 0)에 있다면 시야에 없음을 의미하므로 그리기를 생략하면 되고, 모두 앞쪽(0 < w)에 있다면 그대로 그냥 그리면 된다.
모든 상황을 고려해 동차 좌표계 상에서 삼각형을 분할하는 작업은 다음과 같다.
1. 잘라낼 영역에 몇 개의 점이 속해 있는지 파악한다.
2. 잘라낼 영역에 점이 없으면 그대로 그린다.
3. 잘라낼 영역에 한 점이 속하면, 평면과의 교차점을 구하고 교차점으로부터 삼각형을 두 개로 분할한다.
4. 잘라낼 영역에 두 점이 속하면, 교차점을 구해 갱신한다.
5. 잘라낼 영역에 세 점이 속하면, 그리지 않는다.
절두체의 오른쪽 평면은 NDC 좌표의 값이 언제나 1인 평면인데, 이를 클립 좌표계로 표현하면 다음과 같다.
삼각형을 잘라내는 평면의 식이 w = 0에서 w = x로 바뀌었을 뿐, 잘라내는 원리는 동일하다.
위에서는 잘라낼 영역을 파악하기 위해 음의 영역 w < 0을 사용했는데, 이번에는 w < x를 사용한다.
점 C와 B의 x값을 각각 x.C, x.B로 지정하고 잘라내는 점의 x값을 x.B'이라고 할 때, x.B'은 다음과 같다.
- w.B'에 대해서도 동일하다.
오른쪽 절두체 평면에서는 w = x이므로, 두 값은 같다.
이 식으로부터 t₁에 대해 정리하면 다음과 같다.
t₁의 값을 통해 오른쪽 절두체 평면 w = x에 위치한 점 B', A'의 좌표를 구할 수 있고 삼각형을 자를 수 있게 되었다.
같은 방법으로 절두체를 구성하는 각 평면마다 삼각형 자르기를 진행하면, 아무리 큰 삼각형이라도 절두체 영역에 들어맞는 다각형으로 만들 수 있다.
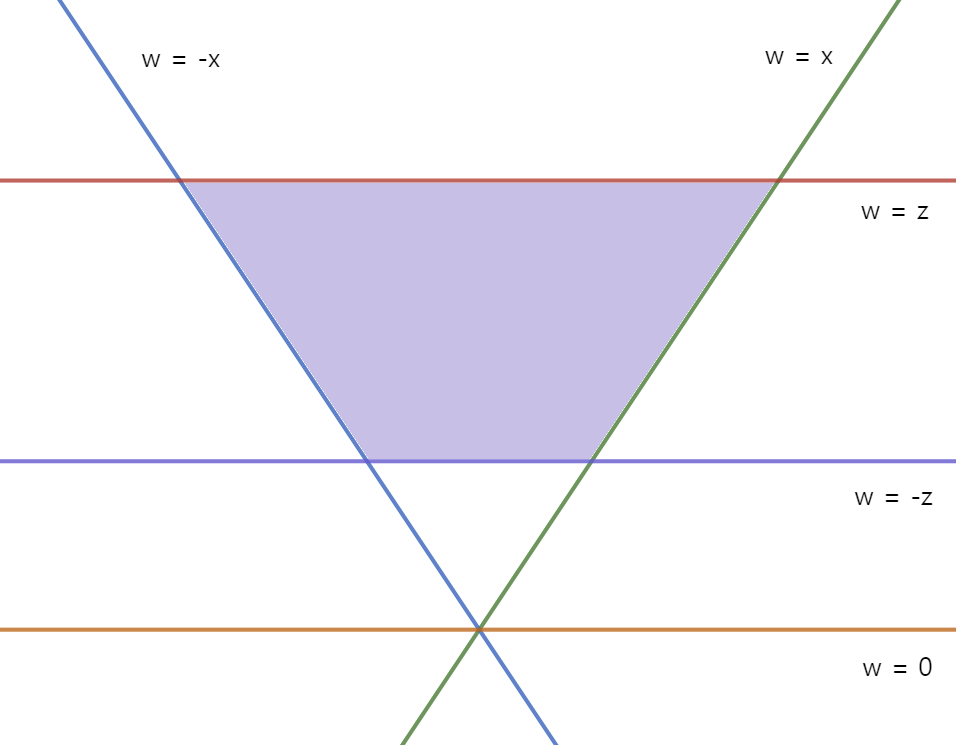
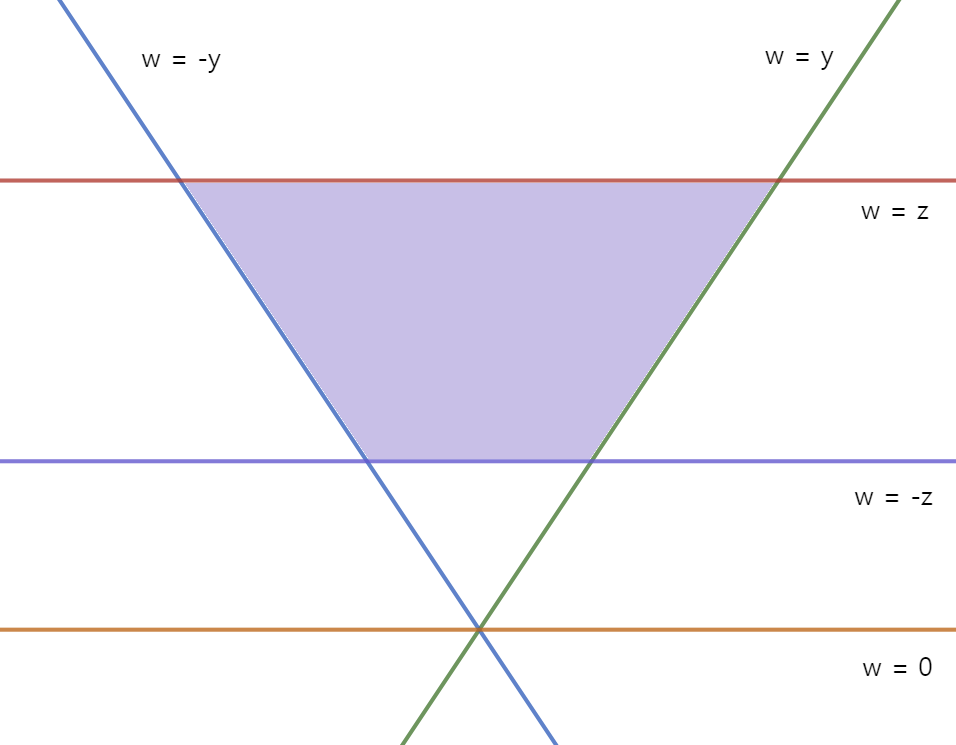
절두체를 구성하는 각 평면의 방정식과 외부 영역에 대한 판별식, 아핀 결합 P = P₁·(1 - t₁) + P₂·t₁의 계수 t₁을 구하는 수식은 다음과 같다.
책의 예제인 CK소프트렌더러에서 삼각형 클리핑에 사용되는 함수는 다음과 같다.
- EdgeFunc 함수에서 아핀 결합의 계수 t₁을 계산해 사영 평면 위의 좌표 P를 구하고, P를 TestFunc에 전달해 점이 평면의 외부에 있는지 판별한다.
// 책의 예제인 CK소프트렌더러에서 삼각형 클리핑에 사용되는 함수들
static auto TestFuncW0 = [](const Vertex3D& InVertex)
{
return InVertex.Position.W < 0.f;
};
static auto EdgeFuncW0 = [](const Vertex3D& InStartVertex, const Vertex3D& InEndVertex)
{
float p1 = InStartVertex.Position.W;
float p2 = InEndVertex.Position.W;
float t = p1 / (p1 - p2);
return InStartVertex * (1.f - t) + InEndVertex * t;
};
static auto TestFuncNY = [](const Vertex3D& InVertex) {
return InVertex.Position.Y < -InVertex.Position.W;
};
static auto EdgeFuncNY = [](const Vertex3D& InStartVertex, const Vertex3D& InEndVertex)
{
float p1 = InStartVertex.Position.W + InStartVertex.Position.Y;
float p2 = InEndVertex.Position.W + InEndVertex.Position.Y;
float t = p1 / (p1 - p2);
return InStartVertex * (1.f - t) + InEndVertex * t;
};
static auto TestFuncPY = [](const Vertex3D& InVertex) {
return InVertex.Position.Y > InVertex.Position.W;
};
static auto EdgeFuncPY = [](const Vertex3D& InStartVertex, const Vertex3D& InEndVertex)
{
float p1 = InStartVertex.Position.W - InStartVertex.Position.Y;
float p2 = InEndVertex.Position.W - InEndVertex.Position.Y;
float t = p1 / (p1 - p2);
return InStartVertex * (1.f - t) + InEndVertex * t;
};
static auto TestFuncNX = [](const Vertex3D& InVertex) {
return InVertex.Position.X < -InVertex.Position.W;
};
static auto EdgeFuncNX = [](const Vertex3D& InStartVertex, const Vertex3D& InEndVertex)
{
float p1 = InStartVertex.Position.W + InStartVertex.Position.X;
float p2 = InEndVertex.Position.W + InEndVertex.Position.X;
float t = p1 / (p1 - p2);
return InStartVertex * (1.f - t) + InEndVertex * t;
};
static auto TestFuncPX = [](const Vertex3D& InVertex) {
return InVertex.Position.X > InVertex.Position.W;
};
static auto EdgeFuncPX = [](const Vertex3D& InStartVertex, const Vertex3D& InEndVertex)
{
float p1 = InStartVertex.Position.W - InStartVertex.Position.X;
float p2 = InEndVertex.Position.W - InEndVertex.Position.X;
float t = p1 / (p1 - p2);
return InStartVertex * (1.f - t) + InEndVertex * t;
};
static auto TestFuncFar = [](const Vertex3D& InVertex)
{
return InVertex.Position.Z > InVertex.Position.W;
};
static auto EdgeFuncFar = [](const Vertex3D& InStartVertex, const Vertex3D& InEndVertex)
{
float p1 = InStartVertex.Position.W - InStartVertex.Position.Z;
float p2 = InEndVertex.Position.W - InEndVertex.Position.Z;
float t = p1 / (p1 - p2);
return InStartVertex * (1.f - t) + InEndVertex * t;
};
static auto TestFuncNear = [](const Vertex3D& InVertex)
{
return InVertex.Position.Z < -InVertex.Position.W;
};
static auto EdgeFuncNear = [](const Vertex3D& InStartVertex, const Vertex3D& InEndVertex)
{
float p1 = InStartVertex.Position.W + InStartVertex.Position.Z;
float p2 = InEndVertex.Position.W + InEndVertex.Position.Z;
float t = p1 / (p1 - p2);
return InStartVertex * (1.f - t) + InEndVertex * t;
};
삼각형 클리핑을 처리하는 구조체는 다음과 같다.
- 모든 세 점이 안쪽에 있으며 클리핑을 건너뛰고, 한 점이 밖에 있으면 잘라내고 남은 사각형 영역을 두 개의 삼각형으로 나누고, 두 점이 밖에 있으면 잘라내기만 진행하고, 모든 점이 밖에 있으면 그리지 않도록 정점을 제거한다.
// 책의 예제인 CK소프트렌더러에서 삼각형 클리핑을 처리하는 구조체
struct PerspectiveTest
{
std::function<bool(const Vertex3D& InVertex)> ClippingTestFunc;
std::function<Vertex3D(const Vertex3D& InStartVertex, const Vertex3D& InEndVertex)> GetEdgeVertexFunc;
std::array<bool, 3> TestResult;
void ClipTriangles(std::vector<Vertex3D>& InOutVertices)
{
size_t triangles = InOutVertices.size() / 3;
for (size_t ti = 0; ti < triangles; ++ti)
{
size_t startIndex = ti * 3;
size_t nonPassCount = 0;
for (size_t ix = 0; ix < 3; ++ix)
{
TestResult[ix] = ClippingTestFunc(InOutVertices[startIndex + ix]);
if (TestResult[ix])
{
nonPassCount++;
}
}
if (nonPassCount == 0)
{
continue;
}
else if (nonPassCount == 1)
{
DivideIntoTwoTriangles(InOutVertices, startIndex, nonPassCount);
}
else if (nonPassCount == 2)
{
ClipTriangle(InOutVertices, startIndex, nonPassCount);
}
else
{
InOutVertices.erase(InOutVertices.begin() + startIndex, InOutVertices.begin() + startIndex + 3);
triangles--;
ti--;
}
}
}
private:
// 점 하나가 평면의 바깥에 있어 삼각형이 2개로 쪼개지는 경우
void DivideIntoTwoTriangles(std::vector<Vertex3D>& InOutVertices, size_t StartIndex, size_t NonPassCount)
{
// 평면의 바깥에 위치한 점 찾기
BYTE index = 0;
if (!TestResult[0])
{
index = TestResult[1] ? 1 : 2;
}
size_t v1Index = StartIndex + (index + 1) % 3;
size_t v2Index = StartIndex + (index + 2) % 3;
Vertex3D v1 = InOutVertices[v1Index];
Vertex3D v2 = InOutVertices[v2Index];
Vertex3D clipped1 = GetEdgeVertexFunc(InOutVertices[StartIndex + index], v1);
Vertex3D clipped2 = GetEdgeVertexFunc(InOutVertices[StartIndex + index], v2);
InOutVertices[StartIndex] = clipped1;
InOutVertices[StartIndex + 1] = v1;
InOutVertices[StartIndex + 2] = v2;
InOutVertices.push_back(clipped1);
InOutVertices.push_back(v2);
InOutVertices.push_back(clipped2);
}
// 점 두 개가 평면의 바깥에 있어 삼각형의 두 점이 변하는 경우
void ClipTriangle(std::vector<Vertex3D>& InOutVertices, size_t StartIndex, size_t NonPassCount)
{
// 평면의 안쪽에 위치한 점 찾기
BYTE index = 0;
if (TestResult[0])
{
index = !TestResult[1] ? 1 : 2;
}
size_t v1Index = StartIndex + (index + 1) % 3;
size_t v2Index = StartIndex + (index + 2) % 3;
Vertex3D v1 = InOutVertices[v1Index];
Vertex3D v2 = InOutVertices[v2Index];
Vertex3D clipped1 = GetEdgeVertexFunc(InOutVertices[StartIndex + index], v1);
Vertex3D clipped2 = GetEdgeVertexFunc(InOutVertices[StartIndex + index], v2);
InOutVertices[v1Index] = clipped1;
InOutVertices[v2Index] = clipped2;
}
};
삼각형 클리핑을 통해 절두체 평면 밖에 있는 삼각형의 영역이 있는지 확인하고 잘라내어 그린다.
// 책의 예제인 CK소프트렌더러에서 메시를 그리는 함수
void SoftRenderer::DrawMesh3D(const Mesh& InMesh, const Matrix4x4& InMatrix, const LinearColor& InColor)
{
size_t vertexCount = InMesh.GetVertices().size();
size_t indexCount = InMesh.GetIndices().size();
size_t triangleCount = indexCount / 3;
// 렌더러가 사용할 정점 버퍼와 인덱스 버퍼로 변환
std::vector<Vertex3D> vertices(vertexCount);
std::vector<size_t> indice(InMesh.GetIndices());
for (size_t vi = 0; vi < vertexCount; ++vi)
{
vertices[vi].Position = Vector4(InMesh.GetVertices()[vi]);
if (InMesh.HasColor())
{
vertices[vi].Color = InMesh.GetColors()[vi];
}
if (InMesh.HasUV())
{
vertices[vi].UV = InMesh.GetUVs()[vi];
}
}
// 정점 변환 진행
VertexShader3D(vertices, InMatrix);
// 삼각형 별로 그리기
for (int ti = 0; ti < triangleCount; ++ti)
{
int bi0 = ti * 3, bi1 = ti * 3 + 1, bi2 = ti * 3 + 2;
std::vector<Vertex3D> tvs = { vertices[indice[bi0]] , vertices[indice[bi1]] , vertices[indice[bi2]] };
if (useHomogeneousClipping)
{
// 동차 좌표계에서 클리핑을 위한 설정
std::vector<PerspectiveTest> testPlanes = {
{ TestFuncW0, EdgeFuncW0 },
{ TestFuncNY, EdgeFuncNY },
{ TestFuncPY, EdgeFuncPY },
{ TestFuncNX, EdgeFuncNX },
{ TestFuncPX, EdgeFuncPX },
{ TestFuncFar, EdgeFuncFar },
{ TestFuncNear, EdgeFuncNear }
};
// 동차 좌표계에서 클리핑 진행
for (auto& p : testPlanes)
{
p.ClipTriangles(tvs);
}
}
size_t triangles = tvs.size() / 3;
for (size_t ti = 0; ti < triangles; ++ti)
{
size_t si = ti * 3;
std::vector<Vertex3D> sub(tvs.begin() + si, tvs.begin() + si + 3);
DrawTriangle3D(sub, InColor, FillMode::Color);
}
}
}
카메라를 많이 움직일 경우 투영 공간이 뒤집혀 비정상적으로 깨지던 문제를 삼각형 클리핑을 통해 해결했다.

'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 복소평면(Complex plane) (0) | 2023.05.26 |
|---|---|
| 복소수(Complex number) (0) | 2023.05.25 |
| AABB (Axis Aligned Bounding Box) (0) | 2023.05.23 |
| 바운딩 볼륨(Bounding volume) (0) | 2023.05.22 |
| 원근 투영 행렬로부터 평면의 방정식 만들기 (0) | 2023.05.21 |














