이득우의 게임 수학
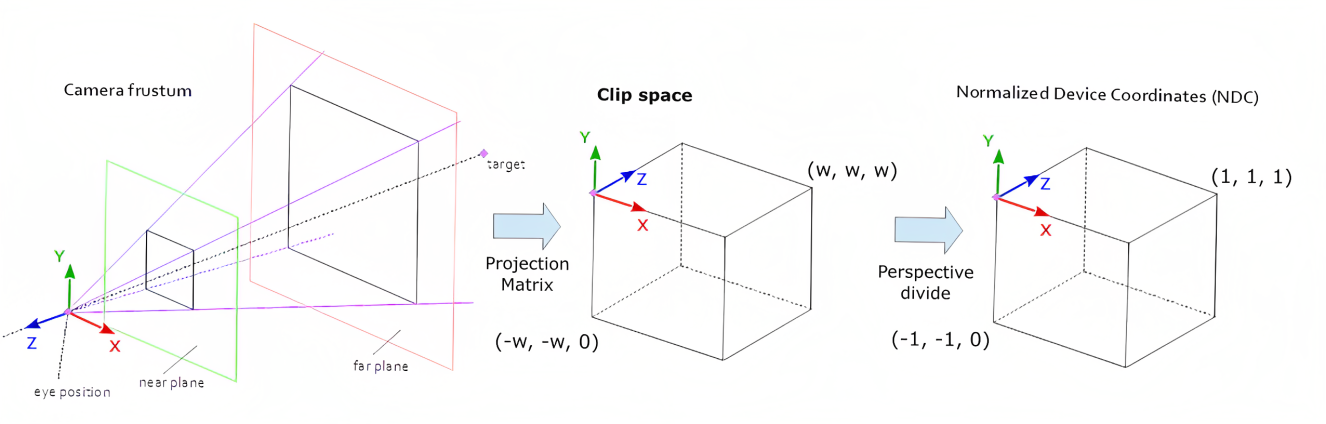
뷰 공간의 점이 NDC 좌표까지 변환됐을 때 NDC 좌표의 x, y, z 값이 [-1, 1] 범위에 있다면, 해당 점은 절두체 안쪽에 있음을 의미한다.

NDC 좌푯값을 수식으로 표현해보면 다음과 같다.

변환 과정을 거꾸로 추적하면서 수식을 살펴본다.
NDC 좌표는 클립 좌표를 마지막 차원의 값 w로 나눈 결과이므로, 클립 좌표로 바꿔 쓰면 다음과 같다.

양 변에 w를 곱한다.

이 상태에서 가꾸로 뷰 공간에서 클립 공간으로 변환한 과정을 살펴본다.
뷰 공간의 점 v를 원근 투영 행렬을 사용해 클립 좌표로 변환하는 수식은 다음과 같다.

원근 투영 행렬을 P.row1부터 P.row4까지 4개의 행 벡터로 표현하면, 위 연산은 행 벡터와 점 v의 내적으로 바꿀 수 있다.

그러면 클립 공간의 각 요소는 행 벡터와 점 v의 내적으로 표현된다.

앞의 부등식을 행 벡터와 점 v의 내적으로 치환하면 다음과 같다.

위 식을 분리하면 절두체의 6면에 해당하는 6개의 부등식을 얻을 수 있다.
- 6개의 부등식이 모두 참이면, 점 v가 절두체 내부에 있음을 의미한다.

위 부등식에서 괄호 안의 두 행 벡터의 연산 결과를 벡터 R(a, b, c, d)로 표현하면, 이를 v(x, y, z, 1)과 내적한 결과는 평면의 방정식과 동일하다.

하지만 이 식에서 만들어지는 법선 벡터 (a, b, c)의 크기는 1이 아니므로, 평면의 방정식을 정규화한다.

절두체 컬링을 구현할 때는 임의의 점이 외부에 있는지 파악하는 수식이 필요하므로, 평면이 절두체 외부를 향하도록 부호를 반전시켜준다.

이제 평면 밖에 위치한 상황을 검출하기 위해 등호 대신 부등호를 써주면 수식이 완성된다.

아래는 책의 예제인 CK소프트렌더러에서 원근 투영 행렬로부터 절두체의 6면에 대한 평면의 방정식을 만들어 내외부를 판정하는 부분이다.
<cpp />
// 책의 예제인 CK소프트렌더러에서 렌더링 로직을 담당하는 함수
void SoftRenderer::Render3D()
{
...
// 렌더링 로직의 로컬 변수
const Matrix4x4 vMatrix = mainCamera.GetViewMatrix();
const Matrix4x4 pMatrix = mainCamera.GetPerspectiveMatrix();
const Matrix4x4 pvMatrix = mainCamera.GetPerspectiveViewMatrix();
// 절두체 구축을 위한 투영 행렬의 설정
Matrix4x4 ptMatrix = pMatrix.Transpose();
// 절두체를 구성하는 평면의 방정식
std::array<Plane, 6> frustumPlanes = {
Plane(-(ptMatrix[3] - ptMatrix[1])), // +Y
Plane(-(ptMatrix[3] + ptMatrix[1])), // -Y
Plane(-(ptMatrix[3] - ptMatrix[0])), // +X
Plane(-(ptMatrix[3] + ptMatrix[0])), // -X
Plane(-(ptMatrix[3] - ptMatrix[2])), // +Z
Plane(-(ptMatrix[3] + ptMatrix[2])) // -Z
};
// 절두체 선언
Frustum frustumInView(frustumPlanes);
for (auto it = g.SceneBegin(); it != g.SceneEnd(); ++it)
{
...
// 절두체 컬링 구현
Vector4 viewPos = vMatrix * Vector4(transform.GetPosition());
if (frustumInView.CheckBound(viewPos.ToVector3()) == BoundCheckResult::Outside)
{
// 그리지 않고 건너뜀
continue;
}
// 최종 행렬 계산
Matrix4x4 finalMatrix = pvMatrix * transform.GetModelingMatrix();
// 메시 그리기
DrawMesh3D(mesh, finalMatrix, gameObject.GetColor());
}
}
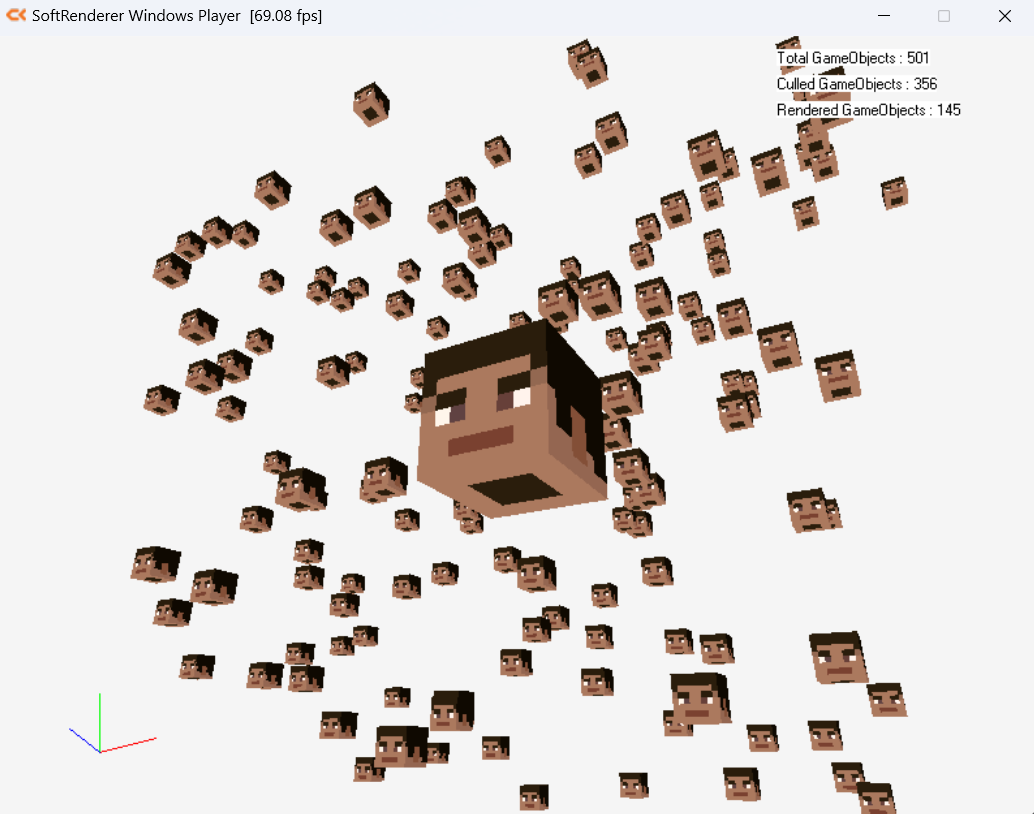
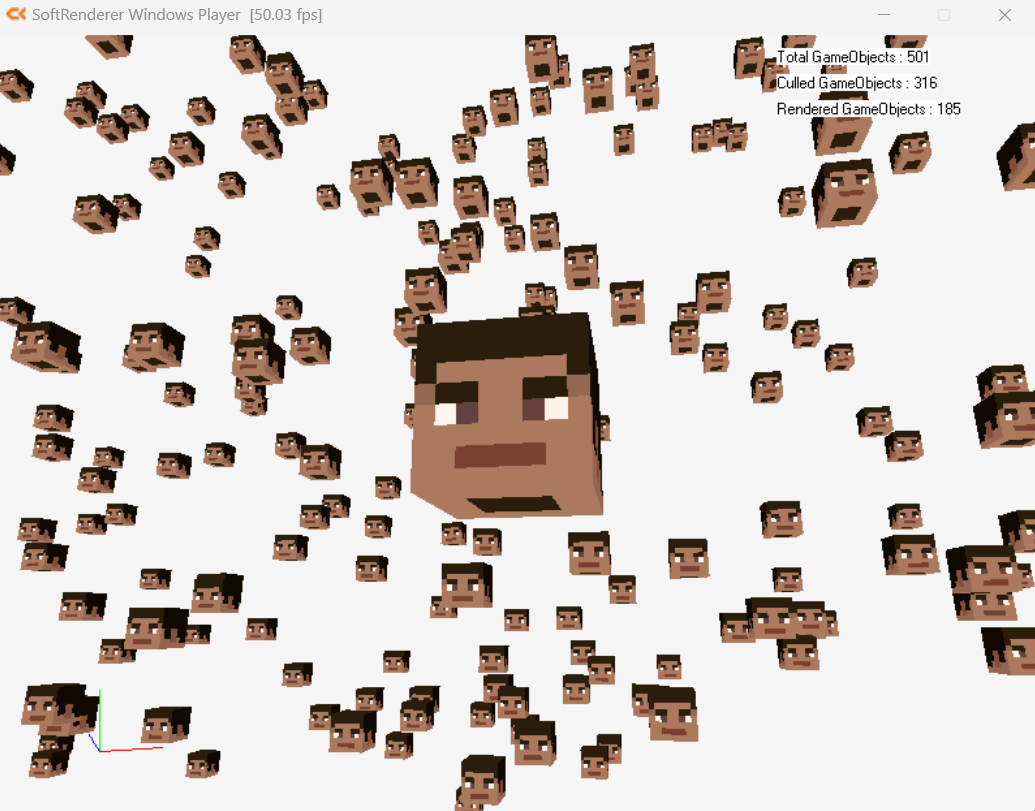
원근 투영 행렬에는 이미 카메라의 종횡비가 반영되어 있기 때문에, 양쪽의 여백은 없어지게 된다.
하지만 여전히 오브젝트의 위치를 이용해 절두체 내외부 판정을 하기 때문에, 가장자리에서 오브젝트가 갑자기 사라지거나 불쑥 생겨나는 현상은 아직 있다.
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| AABB (Axis Aligned Bounding Box) (0) | 2023.05.23 |
|---|---|
| 바운딩 볼륨(Bounding volume) (0) | 2023.05.22 |
| 절두체 컬링(Frustum Culling) (0) | 2023.05.20 |
| 직선의 방정식 (0) | 2023.05.19 |
| 평면의 방정식 (0) | 2023.05.18 |