이득우의 게임 수학
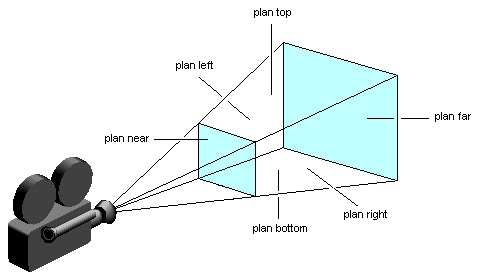
다수의 게임 오브젝트가 월드 공간에 넓게 퍼져 있는 경우, 카메라 시야(절두체) 밖에 위치한 게임 오브젝트까지 모두 그리는 것은 비효율적이다.
그래서 게임에서 그래픽을 구현할 때는 절두체 영역에 속한 게임 오브젝트만을 그리고, 영역 밖에 있는 게임 오브젝트를 파악하고 걸러내는 기능을 절두체 컬링(Frustum culling)이라고 한다.
절두체 컬링은 절두체를 구성하는 6개의 평면에 대해 각각 평면의 방정식을 세워 대상 게임 오브젝트가 평면의 바깥에 있는지 확인하는 정차로 진행된다.
- 6개 평면 중 하나라도 바깥쪽에 위치해 있다면, 그리기에서 제외된다.
절두체 컬링에 앞서 평면의 방정식부터 알아보자.
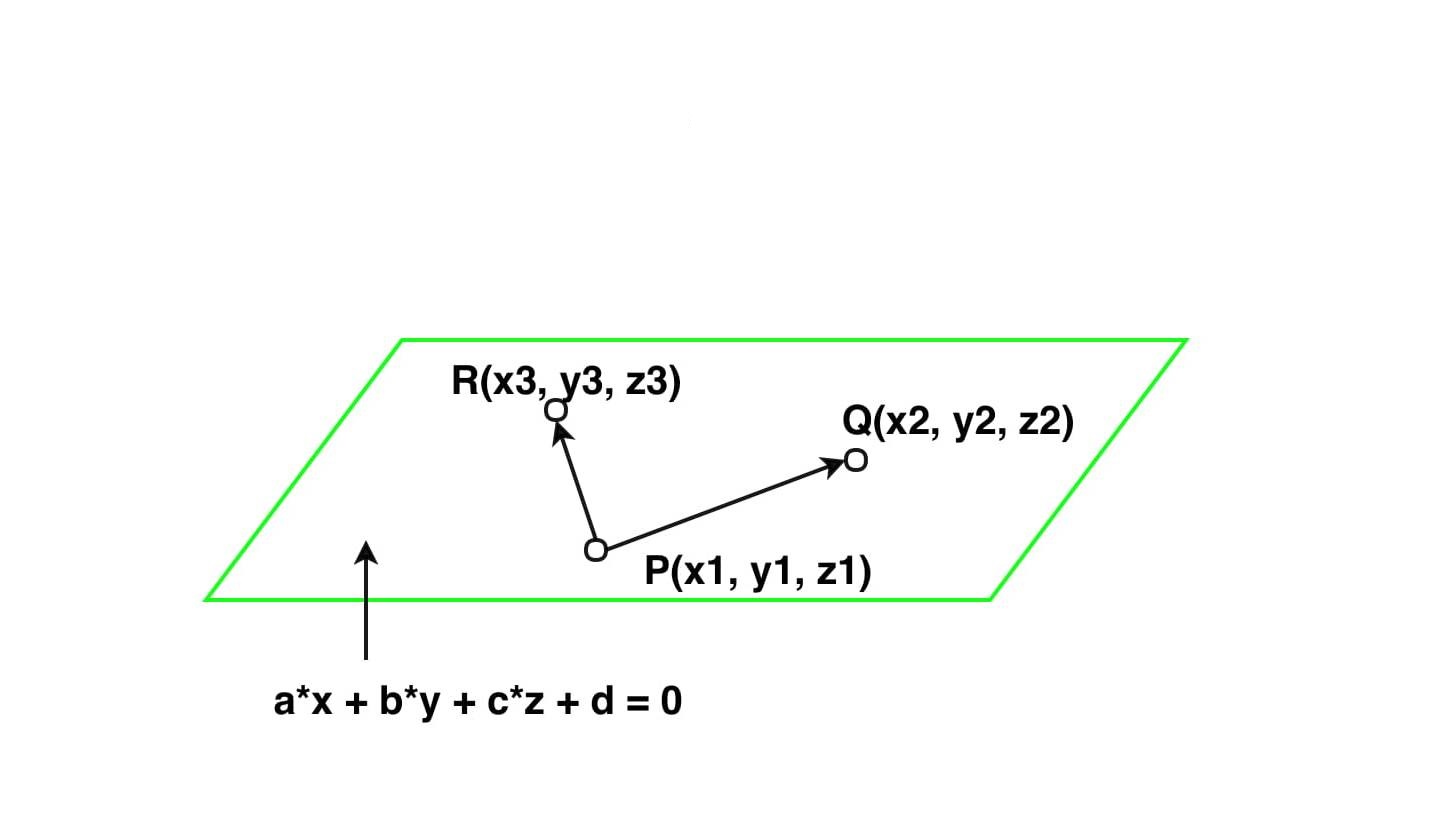
세 점이 주어지면 두 벡터를 생성해 평면 상의 모든 점을 생성할 수 있다.
- 따라서 하나의 평면을 정의하려면 최소 3개의 점이 필요하다.
그런데 3차원 공간의 평면은 앞뒷면이 존재하기 때문에, 방향 정보도 있어야 한다.
그래서 평면을 정의할 때는 세 점보다는 평면의 방향을 알려주는 법선 벡터와 평면 위의 한 점을 활용한다.
- 이때 법선 벡터의 크기는 1로 정규화시키는 것이 일반적이다.
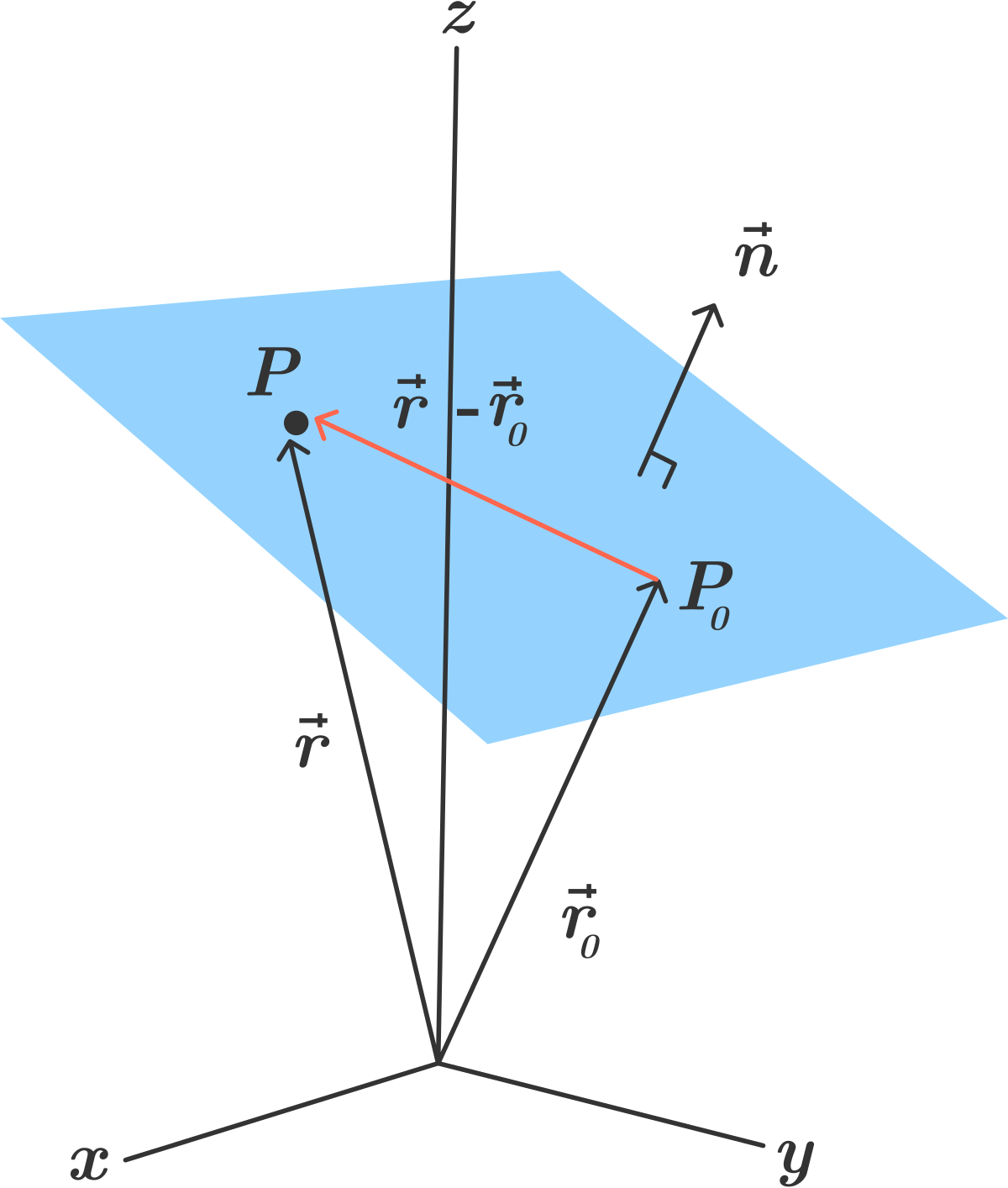
법선 벡터 n(a, b, c)과 평면 위의 점 P₀(x₀, y₀, z₀)로 평면을 정의하고 임의의 점 P(x, y, z)가 같은 평면 위의 있을 조건을 생각해보자.
- a² + b² + c² = 1이다.
평면의 방향을 나타내는 법선 벡터 n과 평면 위의 두 점을 지나는 벡터는 서로 직교하기 때문에, n과 P₀P의 내적이 0이 되면 된다.
여기서 법선 벡터 n(a, b, c)과 평면 위의 점 P₀(x₀, y₀, z₀)는 주어진 값이므로, - (ax₀ + by₀ + cz₀)는 상수이고 이를 d로 치환한다.
d는 법선 벡터 n과 (x₀, y₀, z₀)의 내적에 -1을 곱한 결과로 표현할 수 있다.
그런데 (x₀, y₀, z₀)는 P₀의 좌표지만, 원점 O(0, 0, 0)에서 P₀로 향하는 벡터 p(OP)의 값으로도 표현할 수 있다.
n·p의 의미에 대해 살펴보자.
n은 정규화된 법선 벡터이므로 크기는 1이다.
n·p는 p를 법선 벡터 n에 투영한 벡터의 크기를 의미한다.
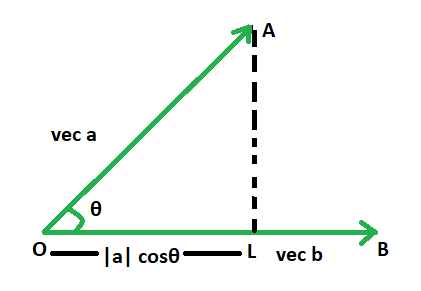
평면과 법선 벡터 n은 서로 직교하기 때문에 n·p의 절댓값은 원점에서 평면까지의 최단 거리를 의미한다.
그러면, d = -n·p의 값은 원점으로부터의 최단 거리와 방향이라는 두 가지 정보를 담고 있음을 알 수 있다.
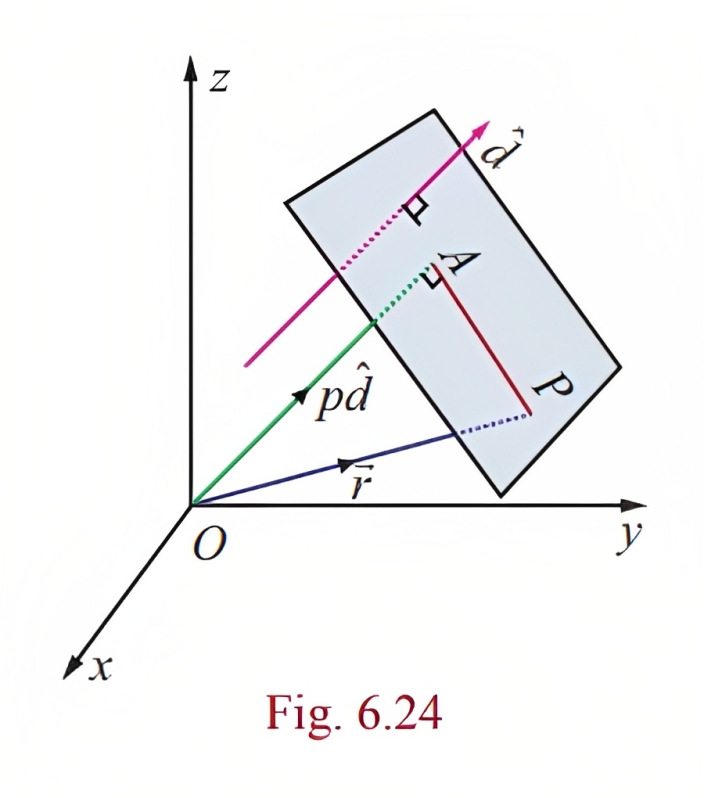
d = -n·p에 음수 부호가 붙어있으므로, d < 0이라면 n과 p가 같은 방향을 바로보고 있다는 의미이며, 평면은 원점의 반대 방향을 바라보고 있다.
0 < d라면 n과 p가 다른 방향을 바라보고 있다는 의미이며 평면은 원점 방향을 바라보고 있다.
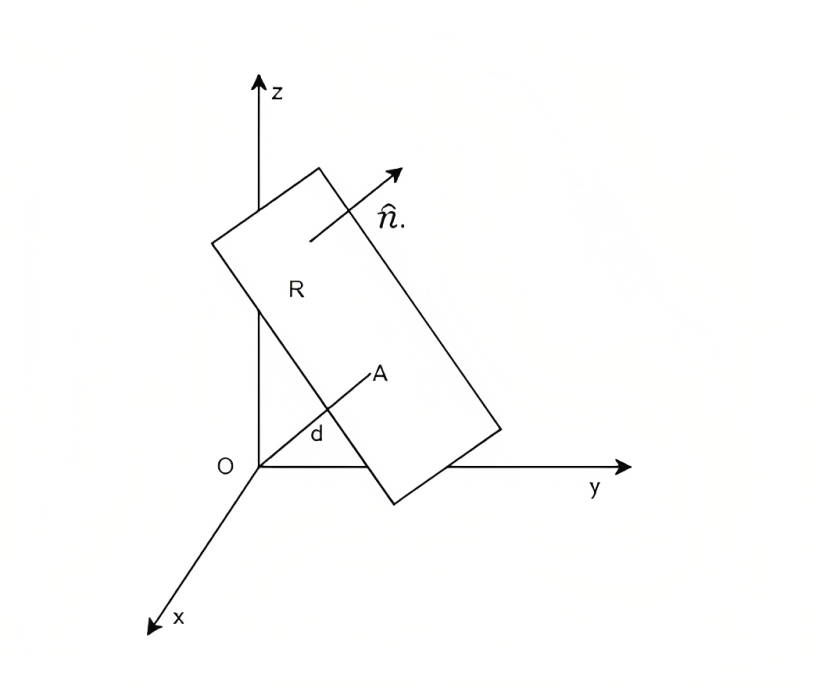
따라서, 법선 벡터 n과 평면 위의 두 점의 벡터인 P₀P의 내적을 평면의 방정식(Equation of a Plane)이라고 한다.
만약 평면 위에 원점이 있다면 거리 d의 값은 부호게 관계없이 항상 0이기 때문에, 법선 벡터 n(a, b, c)의 값만으로도 ax + by + cz = 0이라는 평면의 방정식을 바로 얻을 수 있다.
// 책의 예제인 CK소프트렌더러에 정의된 평면
struct Plane
{
...
public:
Vector3 Normal = Vector3::UnitY;
float D = 0.f;
...
};
평면의 방정식을 구성하는 d의 성질을 이용하면, 3차원 공간의 임의의 점 P가 평면의 안쪽에 있는지 바깥쪽에 있는지도 판별할 수 있다.
원점 O에서 3차원 공간의 임의의 점 P로 향하는 벡터 OP를 법선 벡터 n에 내적한 값을 p라고 하고, 법선 벡터 n에 투영된 P를 P'이라고 하자.
- p의 절댓값은 원점으로부터 P'까지의 거리가 된다.
p가 양수면 OP'은 n과 같은 방향을 향하고, 음수면 반대 방향을 향한다.
이번에는 p + d의 값을 살펴보자.
거리 d < 0이라면, 평면은 원점 방향을 바라보고 있다.
- 이때 d(음수)+ p(양수)의 값이 여전히 음수라면 임의의 점 P는 평면과 원점 사이(평면의 안쪽)에 있다고 할 수 있고, 양수라면 원점과 P 사이(평면의 바깥쪽)에 평면이 있다고 할 수 있다.
거리 d > 0이라면, 평면은 원점의 반대 방향을 바라보고 있다.
- 이때 d(양수)+ p(음수)의 값이 여전히 양수라면 임의의 점 P는 평면과 원점 사이(평면의 바깥쪽)에 있고, 음수라면 원점과 P 사이(평면의 안쪽)에 평면이 있다고 할 수 있고 할 수 있다.

따라서 임의의 점 P(x₁, y₁, z₁)가 법선 벡터 n(a, b, c)과 d로 정의된 평면의 바깥쪽에 있는지, 안쪽에 있는지 판별하는 수식은 다음과 같다.
이 수식에 절댓값을 취하면 평면에서 P까지의 최단 거리가 된다.
// 책의 예제인 CK소프트렌더러에서 평면과 임의의 점까지의 거리 계산과 내외부 판정 로직
struct Plane
{
...
public:
FORCEINLINE constexpr float Plane::Distance(const Vector3& InPoint) const
{
return Normal.Dot(InPoint) + D;
}
FORCEINLINE constexpr bool Plane::IsOutside(const Vector3& InPoint) const
{
return 0.f < Distance(InPoint);
}
...
};
크기가 1이 아닌 법선 벡터 v(a, b, c)가 만들어내는 평면의 방정식이 주어졌다고 해보자.
평면의 방정식도 크기가 1인 법선 벡터로부터 만들어지는 평면의 방정식으로 정규화시킬 수 있다.
크기가 1인 법선 벡터 n(a', b', c')로부터 만들어지는 평면의 방정식은 다음과 같다.
v(a, b, c)를 정규화해 크기가 1인 n(a', b', c')으로 만드는 수식은 다음과 같다.
이번에는 크기가 1이 아닌 벡터 v일 때의 계수 d를, 크기가 1인 벡터 n일 때의 d'으로 바꾸는 수식을 생각해본다.
d는 원점에서 평면 위의 한 점 P로 향하는 벡터 p와 법선 벡터 n을 내적한 값에 음수 부호를 붙인 거리 값이다.
크기가 1인 n일 때의 d'은 다음과 같다.
따라서 d와 d'은 다음 관계가 성립한다.
n과 d' 모두 |v|로 나누면 되므로, 최종적으로 평면의 방정식을 정규화하는 아래 수식을 얻을 수 있다.
평면의 방정식을 정규화시켜주면 d의 값이 원점으로부터의 최단 거리를 의미하기 때문에 유용하다.
// 책의 예제인 CK소프트렌더러에서 임의의 (a, b, c, d)로 구성된 평면의 방정식을 정규화하는 부분
struct Plane
{
...
private:
void Normalize()
{
float squaredSize = Normal.SizeSquared();
if (Math::EqualsInTolerance(squaredSize, 1.f))
{
return;
}
float invLength = Math::InvSqrt(squaredSize);
Normal *= invLength;
D *= invLength;
}
...
};'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 절두체 컬링(Frustum Culling) (0) | 2023.05.20 |
|---|---|
| 직선의 방정식 (0) | 2023.05.19 |
| 깊이 버퍼(Depth buffer) (0) | 2023.05.17 |
| 원근 보정 매핑 (0) | 2023.05.16 |
| 깊이(Depth) (0) | 2023.05.15 |

















