이득우의 게임 수학
근평면, 원평면을 통해 깊이 속성을 추가해 메시에 원근 투영을 해보았다.
이번에는 텍스처를 입혀 본다.
기존에는 아핀 공간에서 텍스처의 색을 선형 보간을 통해 적용하는 아핀 텍스처 매핑(Affine texture mapping) 방식을 사용했지만 여기에는 문제가 있다.

책의 예제인 CK소프트렌더러에서 아핀 텍스처 매핑 방식으로 텍스처를 입히는 부분이다.
// 책의 예제인 CK소프트렌더러에서 삼각형을 그리는 함수
void SoftRenderer::DrawTriangle3D(std::vector<Vertex3D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
...
// 두 점이 화면 밖을 벗어나는 경우 클리핑 처리
lowerLeftPoint.X = Math::Max(0, lowerLeftPoint.X);
lowerLeftPoint.Y = Math::Min(_ScreenSize.Y, lowerLeftPoint.Y);
upperRightPoint.X = Math::Min(_ScreenSize.X, upperRightPoint.X);
upperRightPoint.Y = Math::Max(0, upperRightPoint.Y);
// 삼각형 영역 내 모든 점을 점검하고 색칠
for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
{
for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++y)
{
ScreenPoint fragment = ScreenPoint(x, y);
Vector2 pointToTest = fragment.ToCartesianCoordinate(_ScreenSize);
Vector2 w = pointToTest - InVertices[0].Position.ToVector2();
float wdotu = w.Dot(u);
float wdotv = w.Dot(v);
float s = (wdotv * udotv - wdotu * vdotv) * invDenominator;
float t = (wdotu * udotv - wdotv * udotu) * invDenominator;
float oneMinusST = 1.f - s - t;
// 무게 중심 좌표를 활용해 삼각형에 포함된 픽셀들을 추려낸다.
if ( ((0.f <= s) && (s <= 1.f)) && ((0.f <= t) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)) )
{
Vector2 targetUV = InVertices[0].UV * oneMinusST + InVertices[1].UV * s + InVertices[2].UV * t;
r.DrawPoint(fragment, FragmentShader3D(mainTexture.GetSample(targetUV), LinearColor::White));
}
}
}
}
각 점들의 깊이에 따라 원근 투영이 적용되면서 왜곡이 발생했다.


문제의 원인은 NDC 상의 a와 b의 무게 중심 좌표는 c = 0.5인데, 사영 공간 상의 A와 B의 무게 중심 좌표는 C < 0.5가 되기 때문이다.
사영 공간과 NDC의 무게 중심 좌표가 서로 차이나는 이유는 NDC 공간으로의 변환 과정에서 사영 공간의 마지막 요소인 w의 값 -v.z를 나눴기 때문이다.
- 이는, 투영된 점은 사영 공간의 점이 카메라로부터 가까울수록 원점에서 멀어지고, 카메라로부터 멀어질수록 원점에 가까워지는 반비례 관계로부터 기인한다.
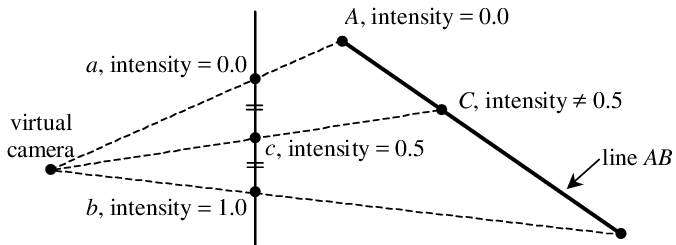
이를 바로잡기 위해서는 투영되기 전 사영 공간에서의 무게 중심 좌표를 사용해야 한다.
따라서, 투영 과정을 거꾸로 추적해 NDC에서 구한 무게 중심 좌표로부터 사용 공간의 무게 중심 좌표를 알아내야 한다.
- 이렇게 투영 전의 무게 중심 좌표 값을 계산해 텍스처를 매핑하는 방식을 투영 보정 보간(Perspective correct interpolation)이라고 한다.
NDC의 무게 중심 좌표를 사영 공간의 무게 중심 좌표로 역추적하는 계산식을 유도하기 위해서는 반비례 함수가 가진 성질을 살펴봐야 한다.
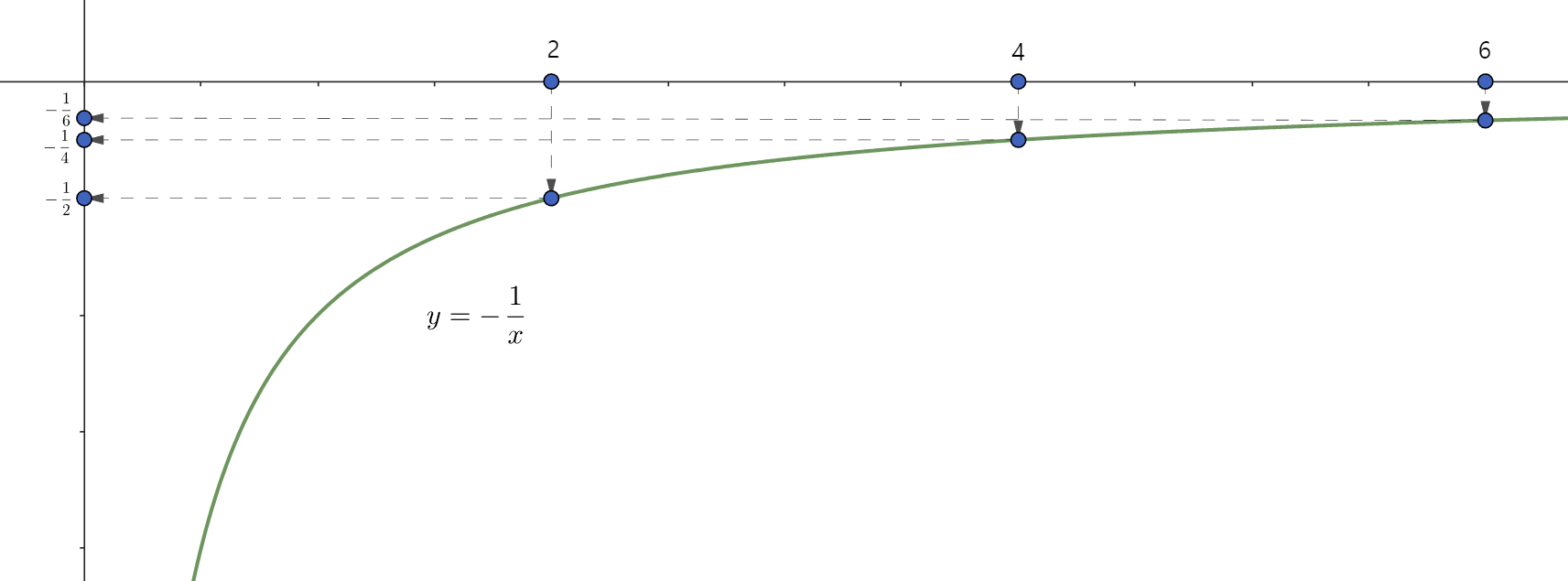
x축에 위치한 세 수 중 가운데 위치한 4의 무게 중심 좌표는 다음 식에 의해 0.5가 된다.
x값 4에 대응하는 y값 -1/4의 무게 중심 좌표는 0.25가 된다.
만일 y축의 무게 중심 좌표 0.25로부터 x축의 무게 중심 좌표 0.5를 계산해주는 식을 찾을 수 있다면, 이를 응용해 사영 공간에서의 무게 중심 값을 계산할 수 있을 것이다.
y축의 두 점 y₁, y₂에 대응하는 무게 중심 좌표를 q₁, q₂로 지정하고, 이를 이용해 사이의 점 y'을 구하는 식은 다음과 같다.
- 무게 중심 좌표의 정의에서 두 무게 중심 좌표의 합 q₁ + q₂ = 1이다.
y의 식을 x로 표현하면 다음과 같다.
x'에 대해 정리하면 다음과 같다.
y₁, y₂의 값과 둘의 무게 중심 좌표 q₁, q₂를 이용해 x'을 계산할 수 있음을 알았다.
양변에 분모를 곱하면 다음 식이 성립한다.
x축의 두 점 x₁, x₂에 대응하는 무게 중심 좌표를 t₁, t₂로 지정하고, 이를 이용해 사이의 점 x'을 구하는 식은 다음과 같다.
- 무게 중심 좌표의 정의에서 두 무게 중심 좌표의 합 t₁ + t₂ = 1이다.
두 무게 중심 좌표의 합이 1임을 이용해위 식을 변환하면 다음과 같다.
양변의 덧셈항을 분리하면 x축의 무게 중심 좌표와 y축의 무게 중심 좌표 간의 관계를 얻을 수 있다.
위 식에 y축에서의 무게 중심 좌표 y₁ = 0.25, y₂ = 0.75를 대입해 확인해본다.
두 점의 조합에 대한 무게 중심 좌표를 확장해 삼각형을 구성하는 세 점의 조합에도 동일하게 적용할 수 있다.
사영 공간에서 NDC로 변환할 때 나누는 값은 뷰 공간의 z값이므로, 위 식에서 x를 z로 치환하면 최종 투영 보간 식을 얻을 수 있다.
이 투영 보정 보간 식을 활용해 아핀 텍스처 매핑의 왜곡을 보정하는 것이 앞에서 말한 원근 보정 매핑이다.
// 책의 예제인 CK소프트렌더러에서 원근 보정 매핑을 적용해 삼각형을 그리는 함수
void SoftRenderer::DrawTriangle3D(std::vector<Vertex3D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
...
// 두 점이 화면 밖을 벗어나는 경우 클리핑 처리
lowerLeftPoint.X = Math::Max(0, lowerLeftPoint.X);
lowerLeftPoint.Y = Math::Min(_ScreenSize.Y, lowerLeftPoint.Y);
upperRightPoint.X = Math::Min(_ScreenSize.X, upperRightPoint.X);
upperRightPoint.Y = Math::Max(0, upperRightPoint.Y);
// 각 정점마다 보존된 뷰 공간의 z값
float invZ0 = 1.f / InVertices[0].Position.W;
float invZ1 = 1.f / InVertices[1].Position.W;
float invZ2 = 1.f / InVertices[2].Position.W;
// 삼각형 영역 내 모든 점을 점검하고 색칠
for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
{
for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++y)
{
ScreenPoint fragment = ScreenPoint(x, y);
Vector2 pointToTest = fragment.ToCartesianCoordinate(_ScreenSize);
Vector2 w = pointToTest - InVertices[0].Position.ToVector2();
float wdotu = w.Dot(u);
float wdotv = w.Dot(v);
float s = (wdotv * udotv - wdotu * vdotv) * invDenominator;
float t = (wdotu * udotv - wdotv * udotu) * invDenominator;
float oneMinusST = 1.f - s - t;
// 무게 중심 좌표를 활용해 삼각형에 포함된 픽셀들을 추려낸다.
if ( ((0.f <= s) && (s <= 1.f)) && ((0.f <= t) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)) )
{
// 투영 보정에 사용할 공통 분모
float z = invZ0 * oneMinusST + invZ1 * s + invZ2 * t;
float invZ = 1.f / z;
Vector2 targetUV = (InVertices[0].UV * oneMinusST * invZ0 + InVertices[1].UV * s * invZ1 + InVertices[2].UV * t * invZ2) * invZ;
r.DrawPoint(fragment, FragmentShader3D(mainTexture.GetSample(targetUV), LinearColor::White));
}
}
}
}
각 점들의 깊이에 따라 사영 공간에서의 무게 중심 좌표를 계산해 원근 보정 매핑을 적용하면서 왜곡이 사라졌다.


'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 평면의 방정식 (0) | 2023.05.18 |
|---|---|
| 깊이 버퍼(Depth buffer) (0) | 2023.05.17 |
| 깊이(Depth) (0) | 2023.05.15 |
| 동차 좌표계 (0) | 2023.05.14 |
| 원근 투영 변환의 원리 (2) | 2023.05.13 |












