이득우의 게임 수학
원근 투영 행렬을 활용해 3차원의 물체를 원근감 있게 표현해봤지만, 텍스처를 입힌다면 추가로 고려할 사항이 발생한다.
카메라의 시선을 기준으로 할 때, 가장 가까운 곳에 위치한 오브젝트를 가장 앞쪽에 그려야 하기 때문이다.
이를 위해 물체가 카메라로부터 얼마나 떨어져 있는지에 대한 정보를 기록해 앞에 있는 물체를 나중에 그리도록 하는 것이다.
- 카메라로부터 얼마나 떨어져 있는지 파악할 수 있는 데이터를 깊이(Dpeth)라고 한다.
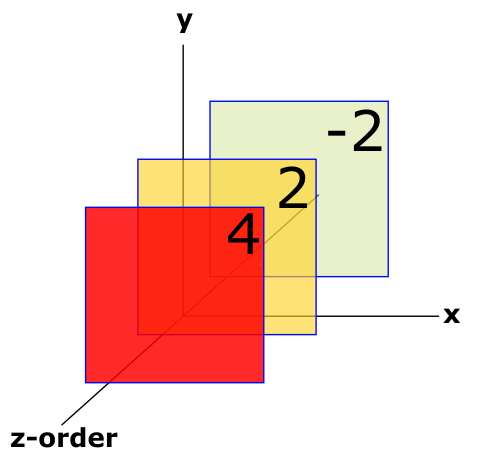

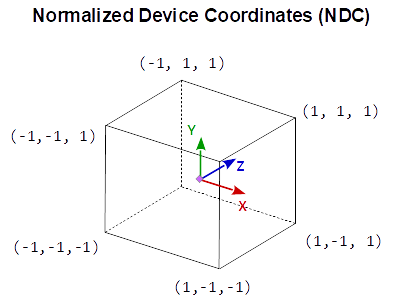
2차원 NDC에 깊이 값을 추가하면 3차원 NDC로 확장된다.
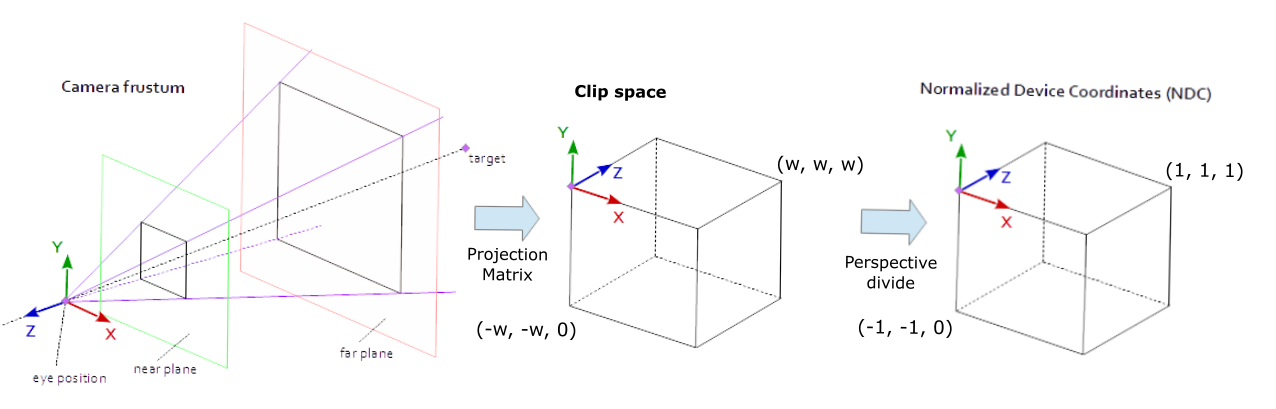
카메라의 속성으로부터 원근 투영 행렬을 생성하기 위해서는 카메라에 추가 속성을 부여해야 한다.
카메라에서 깊이에 대한 속성은 근평면(Near plane)과 원평면(Far plane)으로 나타낸다.
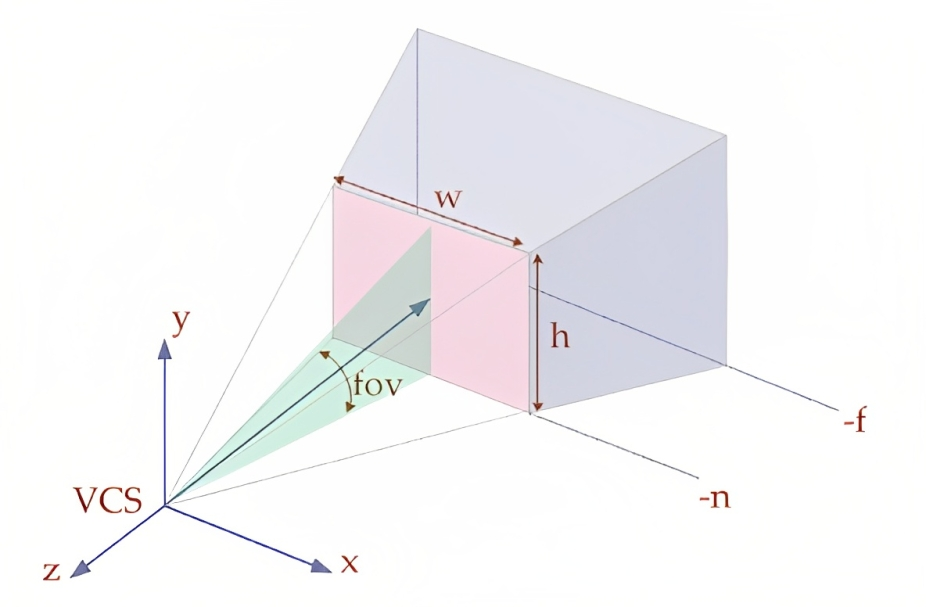
- 카메라의 시야를 구성하는 사영 공간을 근평면과 원평면으로 잘라주면 꼭지가 잘린 피라미드 형태의 절두체(Frustum)가 나온다.
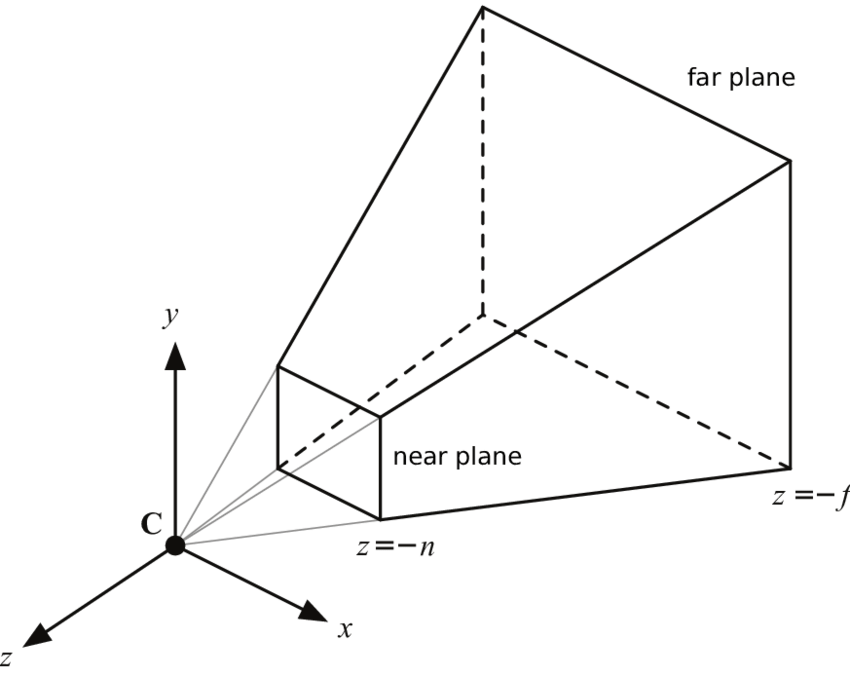
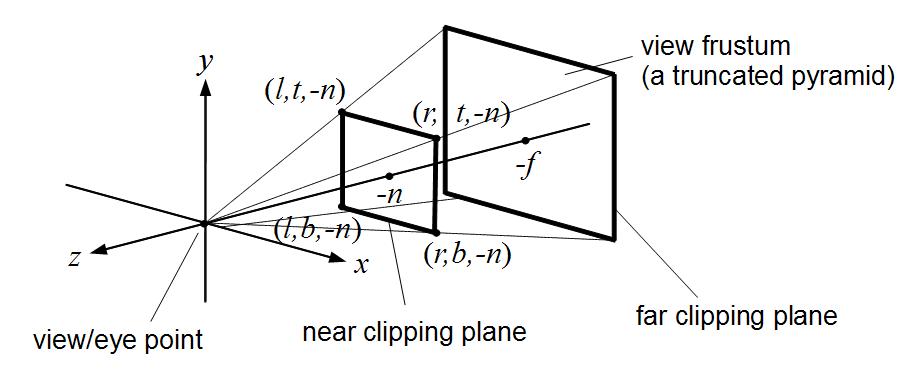
절두체로 생성되는 3차원 NDC 영역에서 깊이 값은 멀어질수록 증가하기 때문에, 왼손 자표계를 형성한다.

기존 원근 투영 해열ㄹ은 다른 행렬과의 곱을 위해 3x3 크기의 행렬을 인위적으로 4x4 크기로 늘렸는데, 이제 깊이 값을 계산할 수 있도록 모든 행렬을 알차게 활용할 수 있게 되었다.
기존 행렬의 3행은 4행으로 옮기고 3행을 깊이 값을 구하는 용도로 변경한다.
깊이 값을 계산하는 데 사용하는 네 개의 미지수를 i, j, k, l로 지정했다.
깊이 값은 뷰 좌표계의 x, y축에 각각 직교하므로 영향을 받지 않기 때문에, i와 j의 값은 0으로 설정한다.
이제 두 미지수 k와 l이 남는데 이를 구하기 위해서는 두 개의 샘플 데이터가 필요하고, 이때 근평면과 원평면의 값을 사용한다.
근평면까지의 거리를 n, 원평면까지의 거리를 f라고 하자.
뷰 공간에서 카메라 중심으로부터 시선 방향으로 n만큼 이동한 근평면 위의 점의 좌표는, 시선 방향이 -z축이기 때문에 (0, 0, -n, 1)이 된다.
- 이는 3차원 NDC에서 깊이 값의 시작 지점이기 때문에 NDC 좌표 (0, 0, -1)에 대응한다.
뷰 공간의 원평만 위의 점의 좌표는 (0, 0, -f, 1)이 되고, 이는 NDC 좌표 (0, 0, 1)에 대응한다.
원근 투영 행렬에 뷰 공간의 점을 곱한 결과는 클립 좌표가 된다.
근평면의 점을 P₁, 원평면의 점을 P₂라고 할 때 다음과 같다.
아직 원근 투영 행렬의 k와 l값을 모르기 때문에 클립 좌표의 세 번째 요소를 계산할 수 없다.
하지만, 클립 좌표의 네 번째 요소로 모든 요소를 나눈 NDC 좌표가 각각 (0, 0, -1), (0, 0, 1)이 됨을 알고 있다.
따라서, (0, 0, ?, n)이 (0, 0, -1)이 되기 위해서는 (0, 0, -n, n)이 되어야 하고, (0, 0, ?, f)가 (0, 0, 1)이 되기 위해서는 (0, 0, f, f)가 되어야 한다.
두 행렬의 3행과 뷰 공간의 점을 내적하면 다음 두 식을 얻을 수 있다.
n과 f는 카메라에 설정된 상수이므로, 두 식을 빼 l을 소거한 후 k를 구하면 다음과 같다.
k를 대입하면 l은 다음과 같다.
k와 l을 대입하면, 깊이 정보를 추가하고 카메라의 속성값만으로 구성된 최종 원근 투영 행렬 P를 구할 수 있다.
- 그렇기 때문에 렌더링 파이프라인의 행렬로 활용할 수 있다.
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 깊이 버퍼(Depth buffer) (0) | 2023.05.17 |
|---|---|
| 원근 보정 매핑 (0) | 2023.05.16 |
| 동차 좌표계 (0) | 2023.05.14 |
| 원근 투영 변환의 원리 (2) | 2023.05.13 |
| 삼중곱(Triple product) (0) | 2023.05.12 |








