이득우의 게임 수학
직선의 방정식 L(a) = a·P₁ + (1 - a)·P₂를 이용해 모니터에 선을 그리면 하나의 픽셀에 다수의 벡터가 대응되기 때문에 비효율적이다.
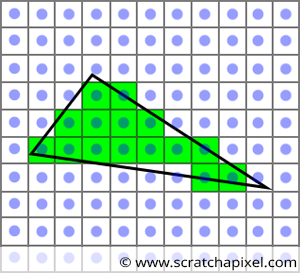
브레젠험 알고리즘은 정수만을 사용해 화면에 선을 그리는 효율적인 알고리즘으로, 화면을 8등분 영역으로 구분해 각 영역별로 그려내는 방식을 사용한다.
- y축이 아래를 향하는 스크린 좌표계에서 구현되므로, 회전의 방향은 시계 방향이 된다.
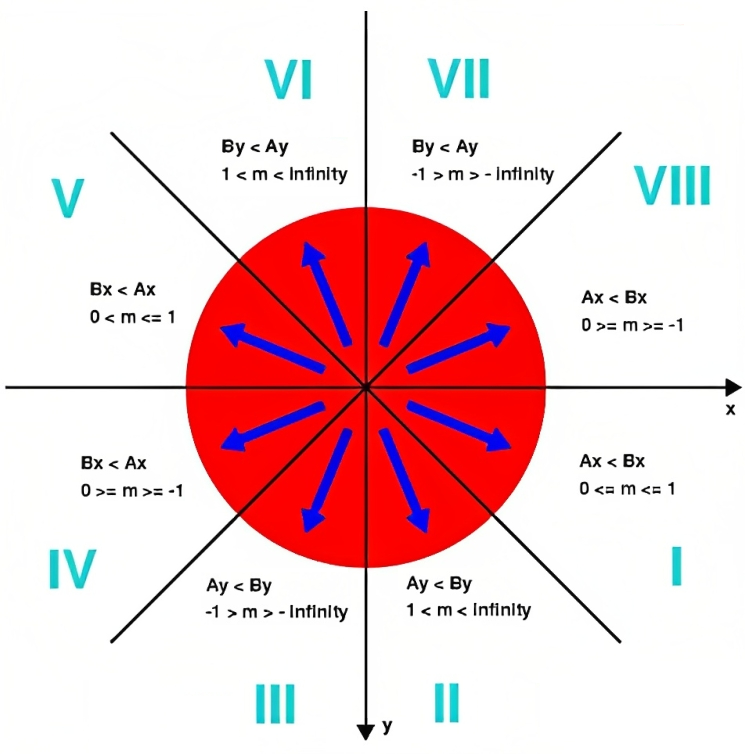

1팔분면(Octant)에 대해 생각해보자.
1팔분면은 [0°, 45°]의 범위를 가지며, 이 영역에 존재하는 모든 직선의 기울기는 1을 넘을 수 없다.
- 그러므로 선을 그리기 위한 진행은 평행하거나, 한 칸만 아래로 내려가는 특징이 있다.
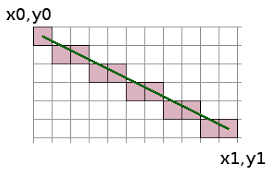
시작 위치 (x₀, y₀)에서 오른쪽으로 한 칸 이동했을 때 될 수 있는 y값은 1팔분면의 특성상 둘 중 하나이다.
- 평행 이동한 y₀
- 한 칸 내려간 y₀ + 1
이 중에서 하나를 선택하기 위해 중간값 y₀ + 0.5를 사용하고, 그래서 브레젠험 알고리즘은 중점 알고리즘(Midpoint algorithm)이라고도 한다.
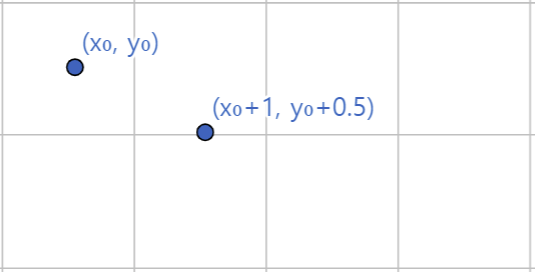
그려야 할 선이 오른쪽으로 한 칸 이동한 중간 점 (x₀ + 1, y₀ + 0.5)보다 위에 있는지, 아래에 있는지 판별하면 된다.
직선의 방정식 y = ax + b에 상수인 시작점 (x₀, y₀)와 직선의 기울기 h/w를 대입하면 다음과 같다.
b로 정리하면 다음과 같다.
기울기와 b가 상수이므로, 직선의 방정식은 다음과 같이 전개된다.
x = x₀ + 1일 때 직선의 방정식으로부터 얻은 y 값이 y₀ + 0.5보다 위에 있는지, 아래에 있는지 판별하면 된다.
이로써, 2h - w < 0인지 비교하는 것만으로 한 칸 이동했을 때의 다음 픽셀의 위치를 계산할 수 있게 됐다.
하지만, 두 칸 이동한 세 번째 픽셀의 판별은 좀 더 까다롭다.
두 번째 픽셀이 평행이동 했다면 세 번째를 판별하기 위한 중간 점은 (x₀ + 2, y₀ + 0.5)가 될 것이고, 한 칸 아래로 내려갔다면 중간 점은 (x₀ + 2, y₀ + 1.5)가 될 것이다.
중간 점이 (x₀ + 2, y₀ + 0.5)인 경우에는 다음 수식을 통해 판별할 수 있다.
중간 점이 (x₀ + 2, y₀ + 1.5)인 경우에는 다음 수식을 통해 판별할 수 있다.
이렇게 계속 진행하다보면, 평행 이동할수록 판별식은 2h만큼 증가하고, 아래로 내려갈수록 2w만큼 감소하는 패턴을 확인할 수 있다.
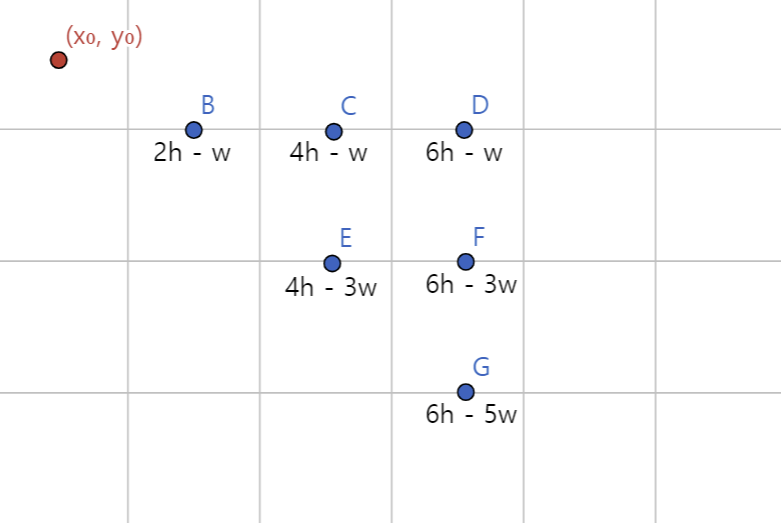
위와 같은 방식으로 각 8분면에 대해 해당하는 기울기를 통해 판별식을 적용하면, 아래와 같은 코드로 직선을 그릴 수 있게 된다.
- <이득우의 게임 수학> 도서의 예제 코드이다.
void WindowsRSI::DrawLine(const Vector2& InStartPos, const Vector2& InEndPos, const LinearColor& InColor)
{
// 시작점, 끝점이 스크린 영역을 벗어나는 경우 클리핑 알고리즘을 통해 영역을 제한한다.
Vector2 clippedStart = InStartPos;
Vector2 clippedEnd = InEndPos;
Vector2 screenExtend = Vector2(_ScreenSize.X, _ScreenSize.Y) * 0.5f;
Vector2 minScreen = -screenExtend;
Vector2 maxScreen = screenExtend;
// 화면 밖에 선분이 존재하는 경우 그릴 필요가 없다.
if (!CohenSutherlandLineClip(clippedStart, clippedEnd, minScreen, maxScreen))
{
return;
}
ScreenPoint startPosition = ScreenPoint::ToScreenCoordinate(_ScreenSize, clippedStart);
ScreenPoint endPosition = ScreenPoint::ToScreenCoordinate(_ScreenSize, clippedEnd);
int width = endPosition.X - startPosition.X;
int height = endPosition.Y - startPosition.Y;
// 기울기를 통해 완만한 경사(true)인지, 급격한 경사(false)인지 저장한다.
bool isGradualSlope = (Math::Abs(width) >= Math::Abs(height));
int dx = (width >= 0) ? 1 : -1;
int dy = (height > 0) ? 1 : -1;
// 판별식에서 사용할 스크린의 너비와 높이이다.
int fw = dx * width;
int fh = dy * height;
// 경사(팔분면)에 따라 초기 판별식을 정한다.
int f = isGradualSlope ? fh * 2 - fw : 2 * fw - fh;
// 수평, 수직 진행인 경우 2h 혹은 2w가 증가하는 추가 판별식이다.
int f1 = isGradualSlope ? 2 * fh : 2 * fw;
// 대각선 진행인 경우 2(h - w) 혹은 2(w - h)가 증가하는 추가 판별식이다.
int f2 = isGradualSlope ? 2 * (fh - fw) : 2 * (fw - fh);
int x = startPosition.X;
int y = startPosition.Y;
// 완만한 경사인 1, 4, 5, 8팔분면의 선을 그린다.
if (isGradualSlope)
{
// 끝점에 도달할 때까지 반복한다.
while (x != endPosition.X)
{
// 픽셀을 채운다.
SetPixel(ScreenPoint(x, y), InColor);
// 판별식이 0보다 작으면 수평, 수직 이동이다.
if (f < 0)
{
f += f1;
}
// 판별식이 0보다 크거나 같으면 대각선 이동이다.
else
{
f += f2;
// 한 칸 아래로 내려간다.
y += dy;
}
// 다음 옆칸으로 진행한다.
x += dx;
}
}
// 급격한 경사인 2, 3, 6, 7팔분면의 선을 그린다.
else
{
// 끝점에 도달할 때까지 반복한다.
while (y != endPosition.Y)
{
// 픽셀을 채운다.
SetPixel(ScreenPoint(x, y), InColor);
// 판별식이 0보다 작으면 수평, 수직 이동이다.
if (f < 0)
{
f += f1;
}
// 판별식이 0보다 크거나 같으면 대각선 이동이다.
else
{
f += f2;
// 한 칸 옆으로 이동한다.
x += dx;
}
// 다음 윗칸으로 진행한다.
y += dy;
}
}
}'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 내적(Dot product) (0) | 2023.04.20 |
|---|---|
| 코헨-서덜랜드 라인 클리핑 알고리즘 (0) | 2023.04.19 |
| 스크린 좌표계(Screen coordinate system) (0) | 2023.04.17 |
| 아핀 결합(Affine Combination) (0) | 2023.04.16 |
| 아핀 공간의 구성 요소 (0) | 2023.04.15 |








