이득우의 게임 수학
아핀 공간의 점은 마지막 차원의 값이 1이어야 하기 때문에, 점과 점은 더하면 2가 되어 더할 수 없다.
하지만, 두 점 P₁(x₁, y₁, 1), P₂(x₂, y₂, 1)에 각각 스칼라 a, b 를 곱해 더하면
- a·P₁ + b·P₂ = (a·x₁ + b·x₂, a·y₁ + b·y₂, a + b)가 된다.
이때 a + b = 1의 조건을 유지한다면, 점과 점의 선형 결합을 통해 새로운 점을 만들 수 있고 이런 결합을 아핀 결합이라고 한다.

아핀 결합은 선형 결합 중에서도, 계수들의 합이 1인 특정한 결합이다.
- 두 점에서 생각해보면, 첫 번째 계수를 a라고 할 때 두 번째 계수는 (1 - a)가 된다.
그러므로 아핀 결합을 통해 생성된 점들 사이에는 특정한 관계가 형성되고, a값을 통해 생성되는 점들을 이어보면 무한히 긴 선이 만들어진다.
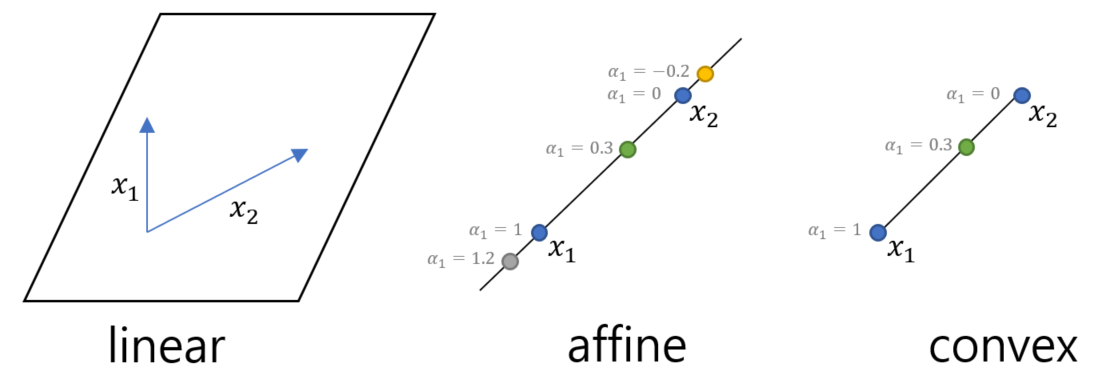
이때 얻어진 선의 수식을 직선의 방정식이라고 한다.
- 직선(Line)
-∞ < a < ∞ - 반직선(Ray)
0 ≤ a < ∞ - 선분(Line Segment)
0 ≤ a ≤ 1
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 브레젠험 알고리즘(Bresenham's algorithm) (0) | 2023.04.18 |
|---|---|
| 스크린 좌표계(Screen coordinate system) (0) | 2023.04.17 |
| 아핀 공간의 구성 요소 (0) | 2023.04.15 |
| 아핀 공간(Affine space) (0) | 2023.04.14 |
| 역행렬 (0) | 2023.04.13 |


