이득우의 게임 수학
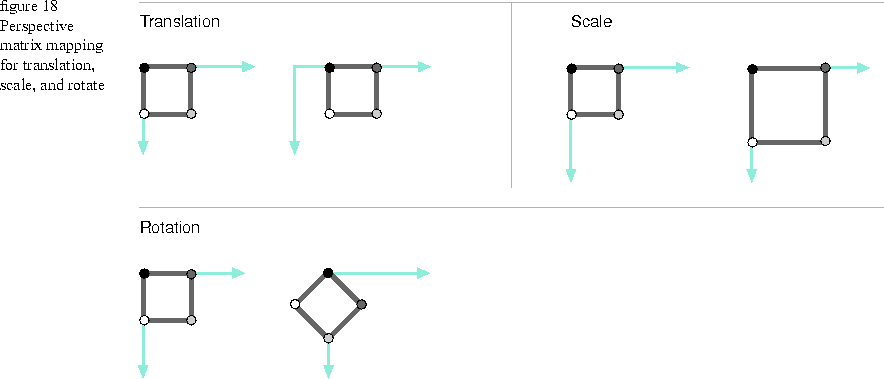
2 x 2 정방 행렬의 곱으로 구현할 수 있었던 크기, 회전 변환과 달리 이동 변환은 그렇지 않다.
임의의 벡터 (x, y)를 (a, b)만큼 이동시킨다고 할 때,
(x, y) + (a, b) = (x + a, y + b)
A·(x, y) = (x + a, y + b)를 만족하는 정방 행렬 A는 존재하지 않는다.
이동 변환과 같이 표준 기저 벡터의 원점을 이동시키는 변환이 행렬이 되기 위해서는 선형성을 만족해야 한다.
이동 이후의 벡터 공간 W의 기저 벡터가 원점으로부터 출발하지 않으므로, 선형성을 만족하지 않기 때문이다.

x값만 이동하는 방법을 생각해보자.
y값을 1로 제한한 특정한 상황에서 x축으로 a만큼 전단 변환을 적용하면, 이동 변환을 구현할 수 있다.
- y를 1로 제한하면, x축으로 a만큼의 전단 변환이 a만큼 이동 변환이 되는 것이다.

이 원리를 2차원 평면에도 적용할 수 있다.
z축을 추가해 1로 제한하면, y축으로 b만큼의 전단 변환은 b만큼의 이동 변환이 된다.

이렇게 마지막 차원의 값이 1인 특정 상황에서의 전단 변환을 통해 이동 변환을 구현할 수 있고, 이때의 행렬을 이동 변환 행렬(Translate transformation matrix)이라고 한다.

이동 변환 행렬에서 주의할 점은, 변환에 사용되는 벡터는 언제나 마지막 차원의 값이 1이어야 한다는 것이다.
- 벡터 (x, y)를 이동 변환하고자 하는 경우에는 사용할 벡터를 (x, y, 1)로 구성해야 한다.
벡터 공간에서 이동을 위해 마지막 차원의 값을 1로 제한한 부분 공간을 아핀 공간이라고 한다.
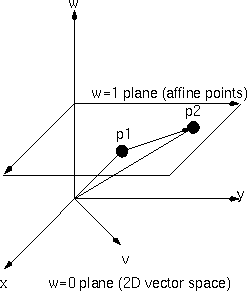
그런데, 평면 상의 벡터 (x, y)의 크기, 회전 변환에 사용되는 행렬은 2 x 2 크기의 정방 행렬이다.
- 행렬 곱의 장점을 살려 최적화 등에 사용하기 위해서는 각 행렬은 크기가 같아야 한다.
따라서 크기, 회전 변환 행렬을 이동 변환에 맞춰 3차원으로 한 차원 높일 필요가 있고, 이렇게 설계한 선형 변환을 아핀 변환(Affine transformation)이라고 한다.
- 각 변환의 결과 역시 마지막 차원의 값이 1로, 아핀 공간에 닫혀 있다.

'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 아핀 결합(Affine Combination) (0) | 2023.04.16 |
|---|---|
| 아핀 공간의 구성 요소 (0) | 2023.04.15 |
| 역행렬 (0) | 2023.04.13 |
| 행렬의 설계 (0) | 2023.04.12 |
| 행렬 (0) | 2023.04.11 |