이득우의 게임 수학
벡터 공간 V를 구성하는 두 표준 기저 벡터 (1, 0), (0, 1)이 선형 변환을 통해, 벡터 공간 W의 (-1, 1), (-1, 3)에 대응되어 변환된다고 해보자.

공간 V의 표준 기저 벡터의 선형 결합으로 생성되는 벡터 v는 공간 W의 벡터 w로 변환된다.
v = x·(1, 0) + y·(0, 1) = (x, y)
w = x·(-1, 1) + y·(-1, 3) = (-1·x + -1·y, 1·x + 3·y)
V의 벡터 v를 W의 벡터 w로 변환시키는 선형 변환 행렬은, V의 표준 기저 벡터 e1(1, 0)과 e2(0, 1)가 변환된 W의 표준 기저 벡터 e1`(-1, 1)과 e2`(-1, 3)의 열벡터로 구성된다는 것을 알 수 있다.

이를 활용해 크기 변환 행렬(Scale transformation matrix)을 설계해보면, 어떤 벡터를 x축으로 a만큼 늘리고 y축으로 b만큼 늘린 벡터는 다음과 같이 표현된다.
e1(1, 0) => e1`(a, 0)
e2(0, 1) => e2`(0, b)
두 표준 기저 벡터 e1`, e2`의 열벡터로 표현하면,
a, 0
0, b

회전 변환 행렬(Rotation transformation matrix)을 설계해보면 다음과 같다.
e1(1, 0) => e1`(cosθ, sinθ)
e2(0, 1) => e2`(-sinθ, cosθ)
두 표준 기저 벡터 e1`, e2`의 열벡터로 표현하면,
cosθ, -sinθ
sinθ , cosθ
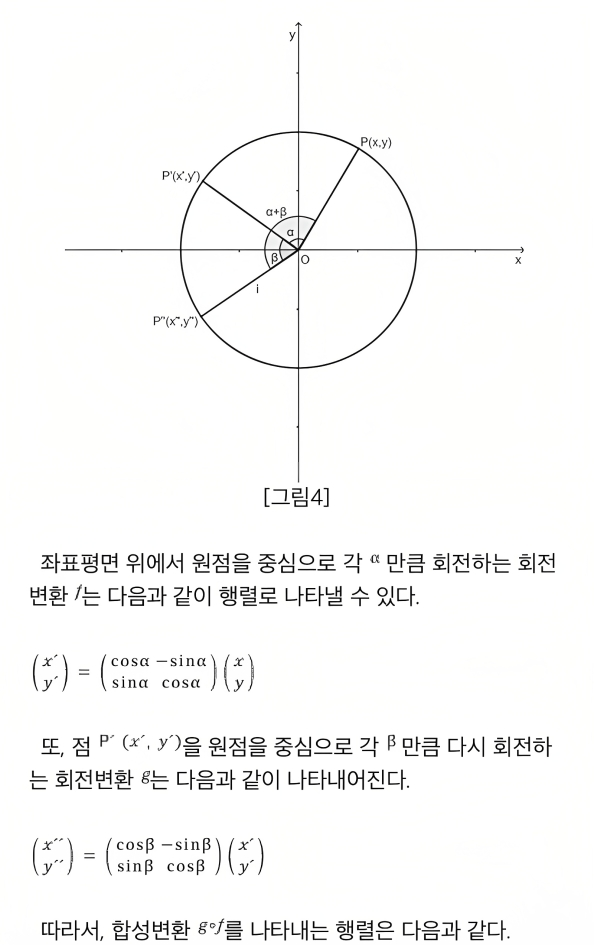
삼각함수의 덧셈 정리도 회전 변환을 활용해 증명할 수 있다.
α+β 만큼의 회전은, β만큼 회전한 후 α만큼 추가로 회전하는 것과 같다.
R(α+β) = R(α)·R(β)
R(α+β)
cos(α+β), -sin(α+β)
sin(α+β) , cos(α+β)
합성 변환 R(α)·R(β)를 행렬의 곱으로 계산하면,
cosα·cosβ - sinα·sinβ , -(cosα·sinβ + sinα·cosβ)
cosα·sinβ + sinα·cosβ, cosα·cosβ - sinα·sinβ
덧셈 정리에 α + α를 대입하면, 배각 공식도 유도할 수 있다.
cos2α = cos(α + α) = cos²α - sin²α = 1 - 2sin²α
sin2α = sin(α + α) = 2·sinα·cosα
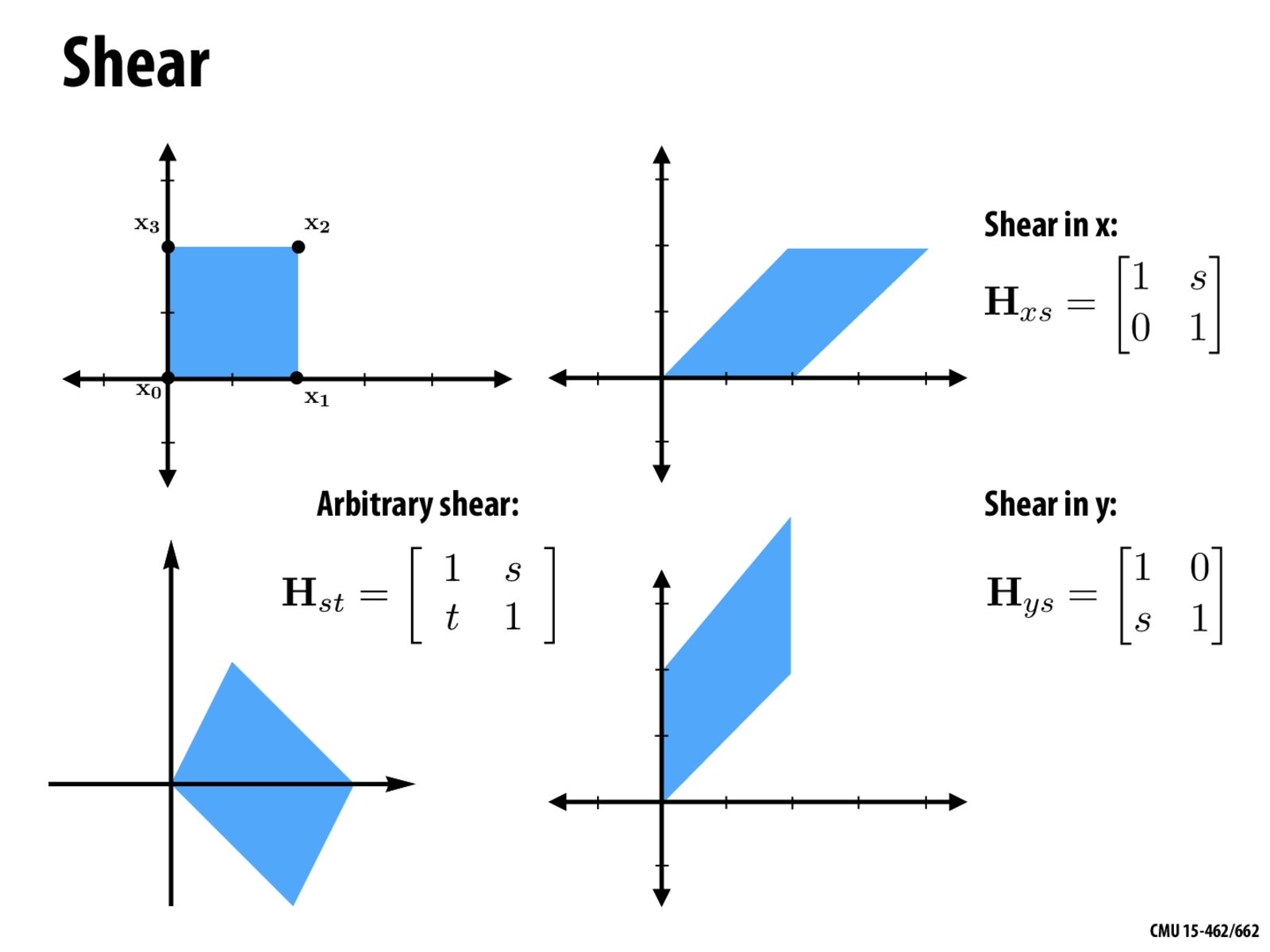
전단 변환 행렬(Shear transformation matrix)을 설계해보면 다음과 같다.
e1을 고정한 상태에서 x축 방향으로 민다고 할 때,
e1(1, 0) => e1`(1, 0)
e2(0, 1) => e2`(b, 1)
두 표준 기저 벡터 e1`, e2`의 열벡터로 표현하면,
1, b
0, 1
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 아핀 공간(Affine space) (0) | 2023.04.14 |
|---|---|
| 역행렬 (0) | 2023.04.13 |
| 행렬 (0) | 2023.04.11 |
| 선형성과 선형 변환 (0) | 2023.04.10 |
| 극좌표계 (0) | 2023.04.09 |

