이득우의 게임 수학
벡터는 한 줄로 구성된 행렬로 표현되며, 행 벡터 또는 열 벡터로 나타낸다.

선형 변환을 표현할 때는 행과 열의 크기가 같은 정방행렬(Square Matrix)을 사용한다.
아래의 회전 변환 행렬의 경우, 각각 행 벡터와 열 벡터로 나타내면 다음과 같다.
| 행 벡터 | cosθ, sinθ | -sinθ, cosθ |
| 열 벡터 | cosθ, -sinθ |
sinθ, cosθ |
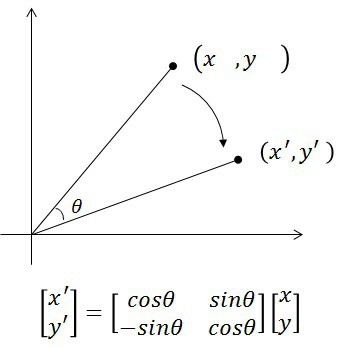
행렬의 덧셈, 뺄셈은 두 행렬의 크기가 같은 경우에만 성립한다.
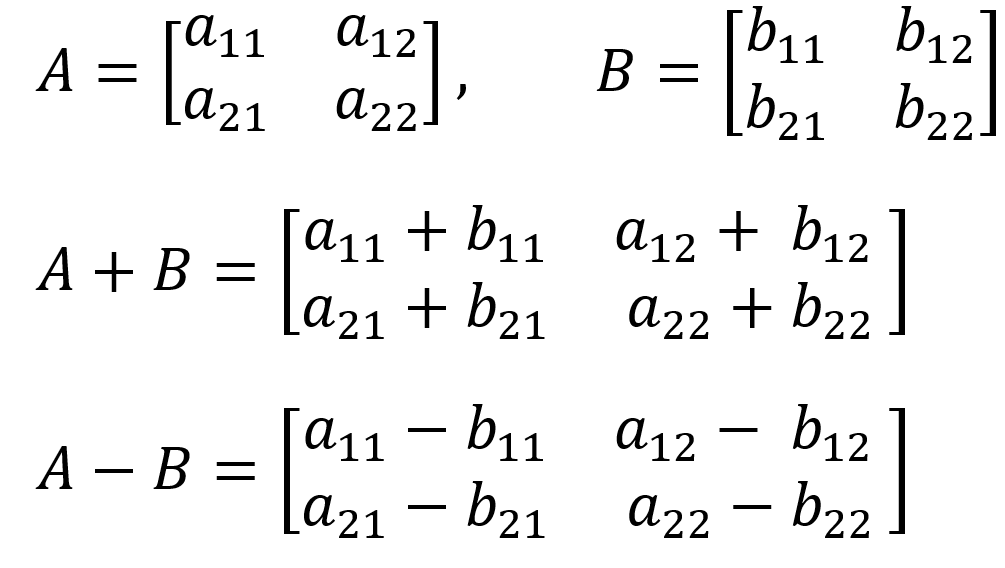
행렬의 스칼라배 연산은 다음과 같다.
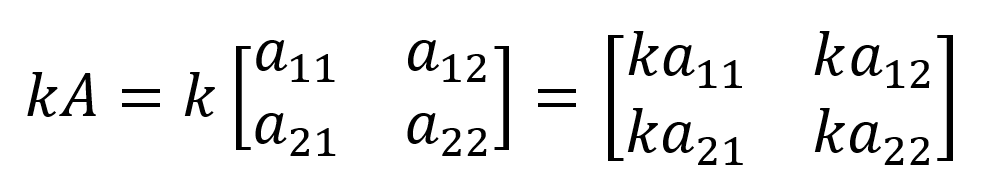
행렬의 전치 연산은 위 첨자 T로 표시하며, 행과 열을 바꾸는 연산이다.
- m x n 크기 행렬에 전치 연산을 수행하면, n x m 크기의 행렬이 된다.
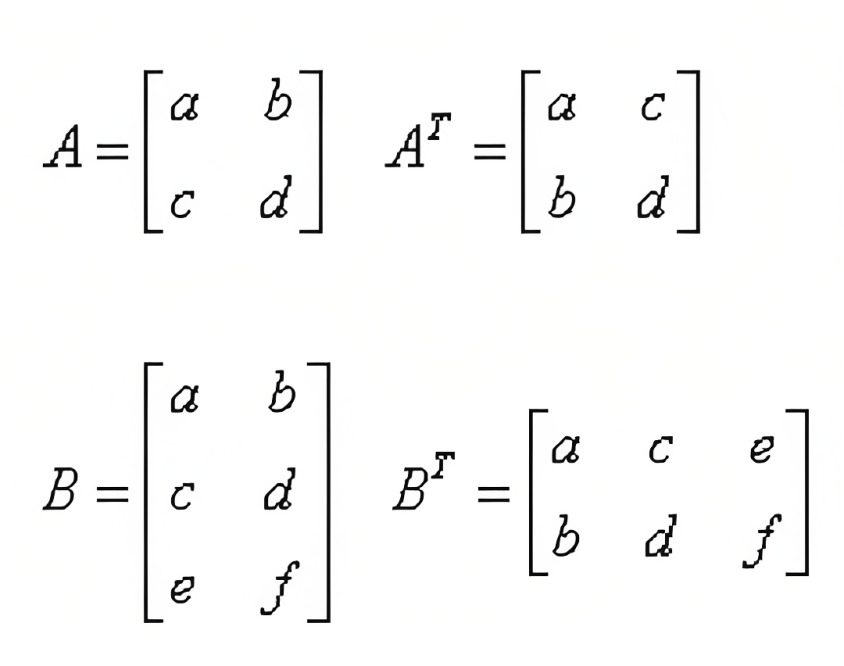
정방 행렬 중에 주 대각선(Principal diagonal) 원소들을 제외하고, 나머지 원소가 모두 0인 정방 행렬을 대각 행렬(Diagonal Matrix)이라고 한다.



이산 수학에서 가장 중요하다고 할 수 있는 행렬의 곱셈 연산은 다음과 같다.
- 앞 행렬의 열의 개수와 뒤 행렬의 행의 개수가 같아야 수행할 수 있다.
- 교환 법칙이 성립하지 않는다.
A·B ≠ B·A - 결합 법칙은 성립한다.
A·(B·C) = (A·B)·C

행렬 곱은 전치 연산에 대해 다음의 특징을 갖는다.
- T(A·B) = T(A)·T(B)
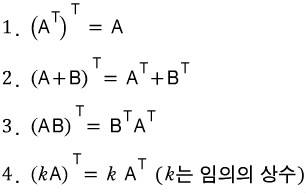
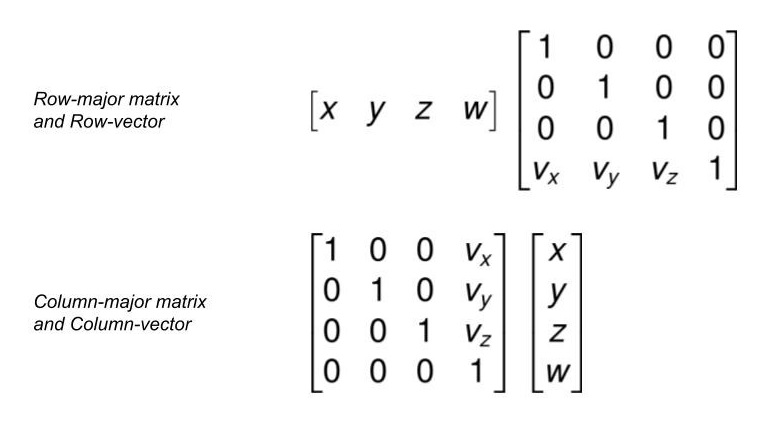
행렬과 벡터의 곱셈을 수행하는 방식으로, 열 기준 행렬(Column major matrix)과 행 기준 행렬(Row major matrix)이 있다.
- 열 기준 행렬 방식
유니티
OpenGL - 행 기준 행렬 방식
언리얼 엔진
DirectX
보통은 열 기준 방식을 많이 사용하고, 각 방식은 행렬과 벡터의 순서가 다르며 서로 전치되어 있다.
행렬 곱에 결합 법칙이 성립한다는 점을 이용해 그래픽 연산에서 최적화에 활용할 수 있다.
100개의 점으로 구성된 물체가 모니터에 출력되기 위해 거치는 선형 변환의 수가 A, B, C, D, E 총 5개라고 해보자.
- 그냥 수행하면 100개 * 5번으로 해서 총 500번의 곱을 수행해야 한다.
하지만, 결합 법칙이 성립한다는 점을 활용하면 변환 F = E·D·C·B·A를 미리 계산할 수 있다.
- 이때는 4번 + 100개 * 1번이 되므로, 104번의 곱으로 최적화할 수 있다.
보통 가상 공간에 하나의 캐릭터를 표현하는 데 약 10만 개의 점(Vertex)이 사용되므로, 최적화는 아주 중요한 요소이다.
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 역행렬 (0) | 2023.04.13 |
|---|---|
| 행렬의 설계 (0) | 2023.04.12 |
| 선형성과 선형 변환 (0) | 2023.04.10 |
| 극좌표계 (0) | 2023.04.09 |
| 삼각함수의 역함수 (0) | 2023.04.08 |
