이득우의 게임 수학
행렬은 본질적으로 함수의 성질을 지니기 때문에, 항등 함수에 대응하는 항등 행렬(Identity Matrix)과 역함수에 대응하는 역행렬(Inverse Matrix)이 존재한다.
항등 행렬
원 공간의 변화 없이 동일한 공간으로 유지하는 변환
따라서, 변환된 공간의 표준 기저 벡터는 원 공간의 표준 기저 벡터와 동일하다.
항등 행렬 I
1, 0
0, 1
역행렬
역원의 개념과 같게, A·T = T·A = I를 만족하는 T이다.
A의 역행렬 T = A⁻¹로 표시한다.
벡터 공간 V가 선형 변환된 벡터 공간 W가 존재할 때, W를 다시 원 벡터 공간 V로 되돌리는 선형 변환이다.

행렬식(Determinant)
어떤 함수가 역함수를 갖기 위해서는 전단사함수여야 한다.
마찬가지로 어떤 행렬이 역행렬을 갖기 위해서는, 두 공간의 변환이 전단사 대응되어야 한다.
행렬 A
a, b
c, d
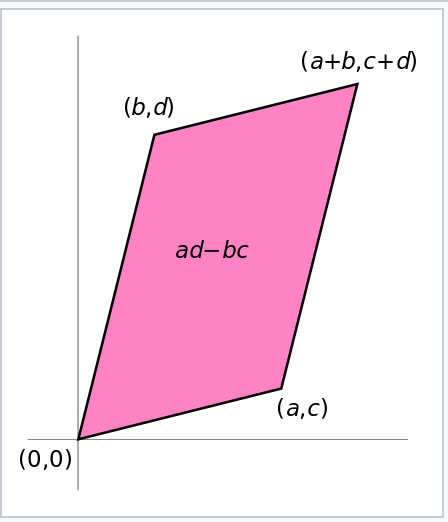
A의 행렬식 det(A) = ad - bc로 계산되며, 0인 경우 역행렬이 존재하지 않는다.
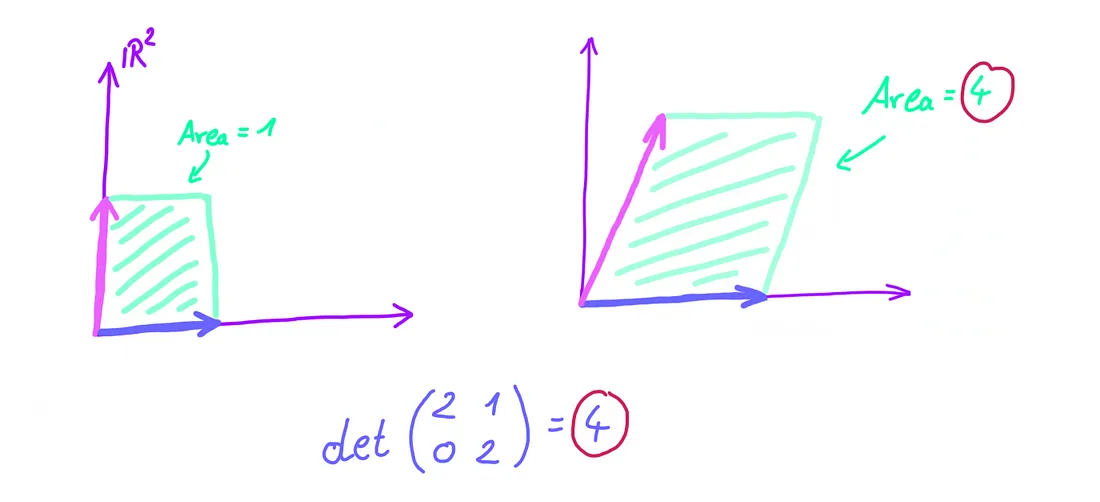
det(A)는 선형 변환 A를 통해 변환된 새로운 벡터 공간의 넓이를 의미한다.
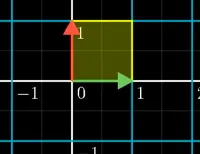
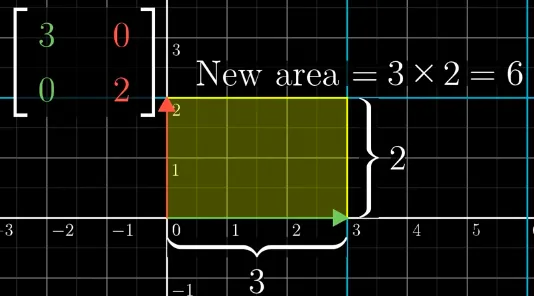
공간 V를 공간 W로 변환하는 선형 변환 A가 다음과 같을 때, V의 표준 기저 벡터 (1, 0), (0, 1)이 W의 표준 기저 벡터 (3, 0), (0, 2)로 변환됨을 알 수 있다.
det(A) = 3·2 - 0·0 = 6이므로 역행렬이 존재한다.
- 공간 V의 벡터가 공간 W의 벡터와 전단사 대응하는 것을 볼 수 있다.
- 따라서, 공간 W로부터 공간 V의 원 벡터를 유추해 볼 수 있다.
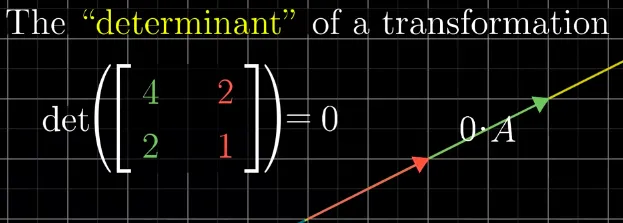
선형 변환 A가 다음과 같을 때, V의 표준 기저 벡터 (1, 0), (0, 1)이 W의 표준 기저 벡터 (4, 2), (2, 1)로 변환됨을 알 수 있다.
det(A) = 4·1 - 2·2 = 0이므로 역행렬이 존재하지 않는다.
- 공간 V의 벡터가 공간 W의 벡터와 전단사 대응하지 않는 것을 볼 수 있다.
- 2차원 평면이 1차원 직선으로 축소되면서 정보가 소멸되어, 공간 W로부터 공간 V의 원 벡터를 유추해 볼 수 없게 되었다.
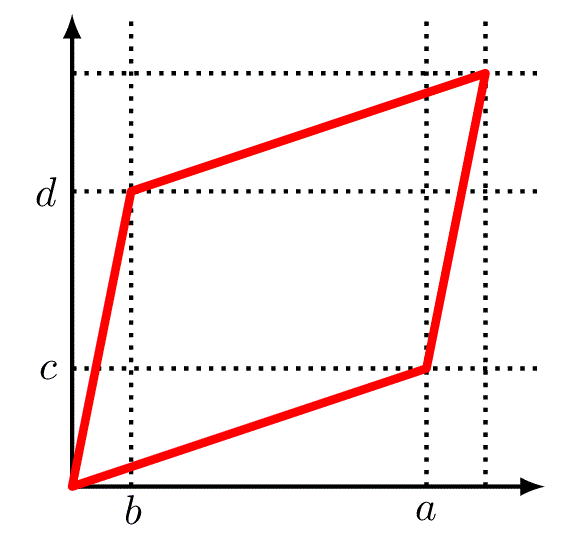
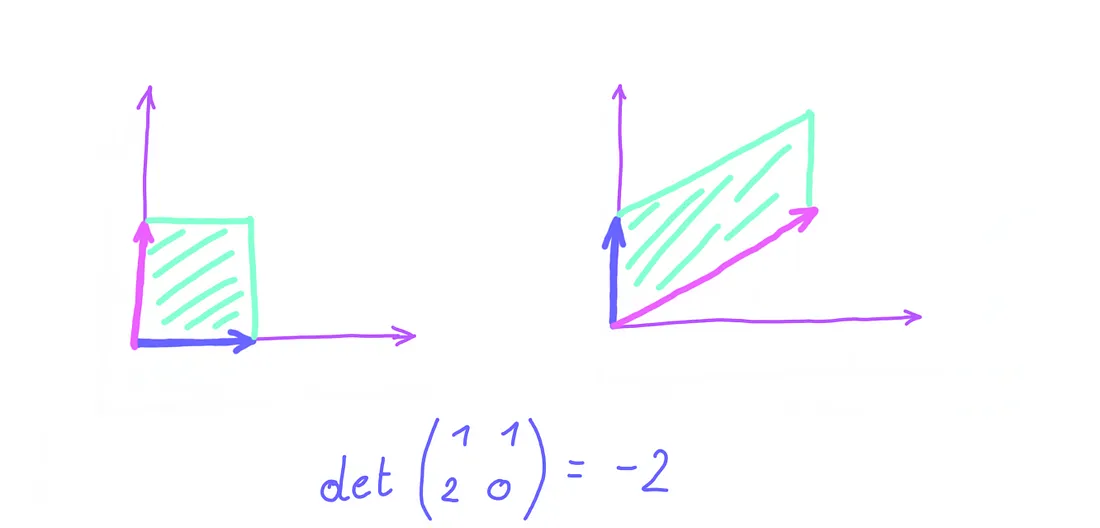
좌측과 같이 a > b이고 d > c라면, ad - bc의 값은 항상 양수가 된다.
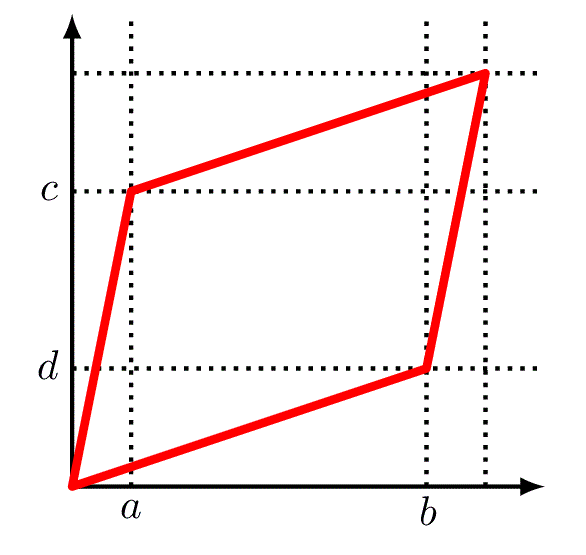
우측과 같이 b > a이고 c > d라면, ad - bc의 값은 항상 음수가 된다.
det(A)의 값이 음수라는 것은, 변환 사이에 표준 기저 벡터의 위/아래과 바뀌면서 평면이 뒤집혔다고 생각할 수 있다.
- 따라서 행렬식의 부호를 통해, 원 공간과 동일한 면으로 설정되어 있는지, 뒤집힌 반대면으로 설정되어 있는지 알 수 있다.
크기 변환의 역행렬
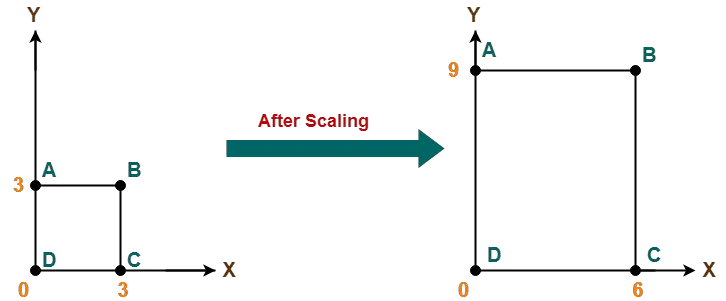
공간 V의 표준 기저 벡터 (1, 0), (0, 1)을 W의 표준 기저 벡터 (a, 0), (0, b)로 변환시키는 선형 변환 A가 있다고 해보자.
선형 변환 A
a, 0
0, b
공간 W를 1/a, 1/b만큼 축소시키면 다시 V가 된다.
W의 표준 기저 벡터 (a, 0), (0, b)를 V의 표준 기저 벡터 (1, 0), (0, 1)로 변환시키는 역행렬 A⁻¹
1/a, 0
0 , 1/b
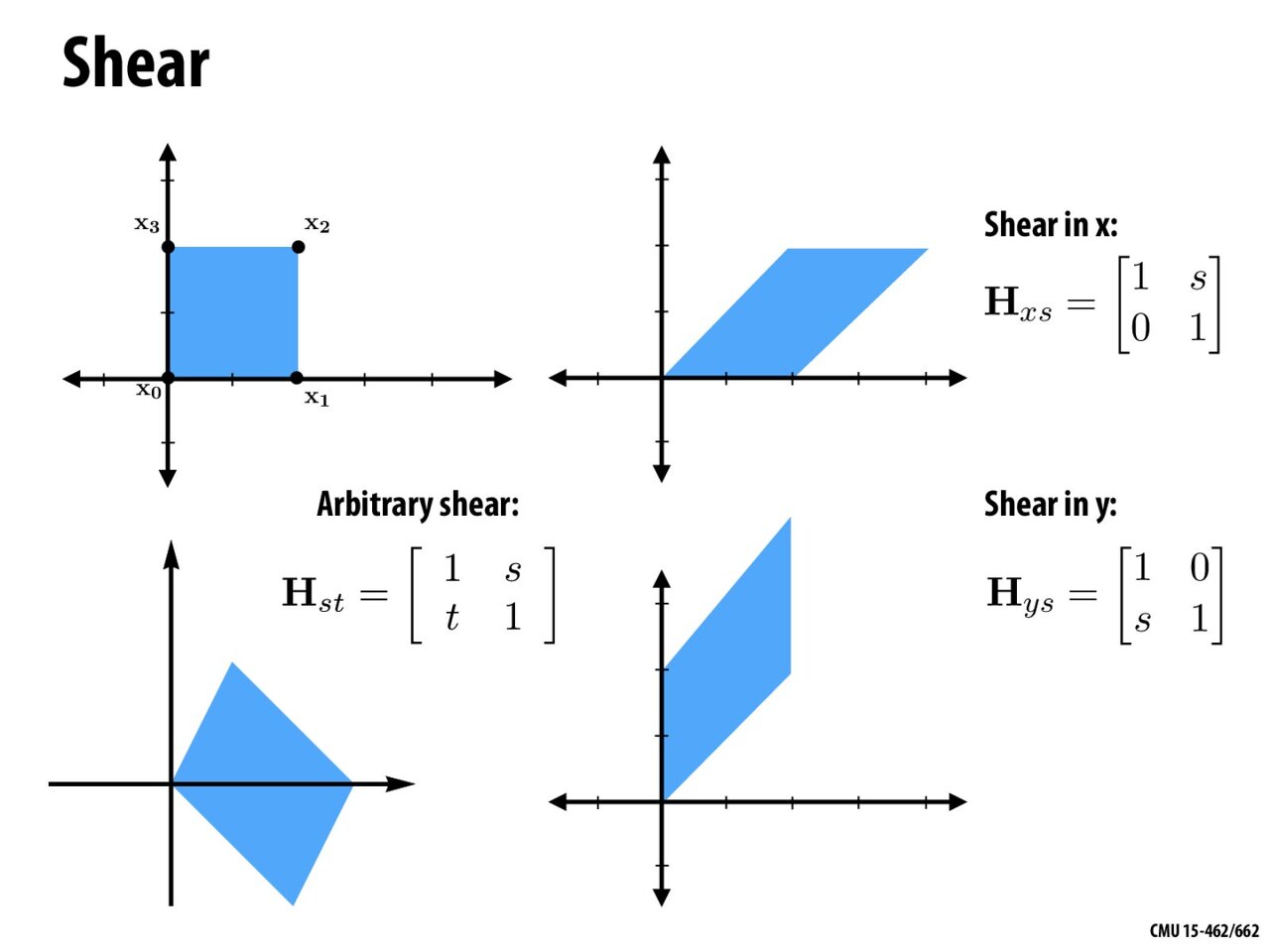
전단 변환 행렬의 역행렬
공간 V의 표준 기저 벡터 (1, 0), (0, 1)을 W의 표준 기저 벡터 (1, 0), (a, 1)로 변환시키는 선형 변환 A가 있다고 해보자.
선형 변환 A
1, a
0, 1
공간 W를 x축으로 -a만큼 밀면 다시 V가 된다.
W의 표준 기저 벡터 (1, 0), (a, 1)를 V의 표준 기저 벡터 (1, 0), (0, 1)로 변환시키는 역행렬 A⁻¹
1, -a
0, 1
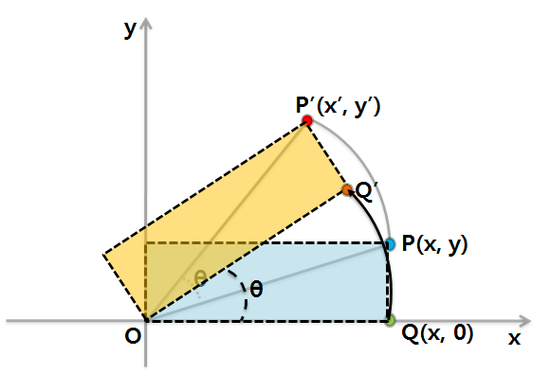
회전 변환 행렬의 역행렬
공간 V의 표준 기저 벡터 (1, 0), (0, 1)을 W의 표준 기저 벡터 (cosθ, sinθ), (-sinθ, cosθ)로 변환시키는 선형 변환 R가 있다고 해보자.
선형 변환 R
cosθ, -sinθ
sinθ , cosθ
공간 W를 -θ만큼 회전하면 다시 V가 된다.
cos(-θ) = cosθ
sin(-θ) = -sinθ
W의 표준 기저 벡터 (cosθ, sinθ), (-sinθ, cosθ)를 V의 표준 기저 벡터 (1, 0), (0, 1)로 변환시키는 역행렬 R⁻¹(θ) = R(-θ)
cos(-θ), -sin(-θ) ==> cosθ, sinθ
sin(-θ) , cos(-θ) ==> -sinθ , cosθ
역행렬 R⁻¹(θ) = R(-θ) = 전치 행렬 T(R(θ))과 같다.
행렬 곱의 역행렬
합성 함수 (g·f)⁻¹ = f⁻¹·g⁻¹이 성립한다.
합성 함수에 해당하는 두 행렬의 곱 (A·B)⁻¹ = B⁻¹·A⁻¹도 동일하게 성립한다.
A·B = C라고 하면,
C·C⁻¹ = I
(A·B)·(A·B)⁻¹ = I
A⁻¹·(A·B)·(A·B)⁻¹ = A⁻¹
B·(A·B)⁻¹ = A⁻¹
B⁻¹·B·(A·B)⁻¹ = B⁻¹·A⁻¹
(A·B)⁻¹ = B⁻¹·A⁻¹
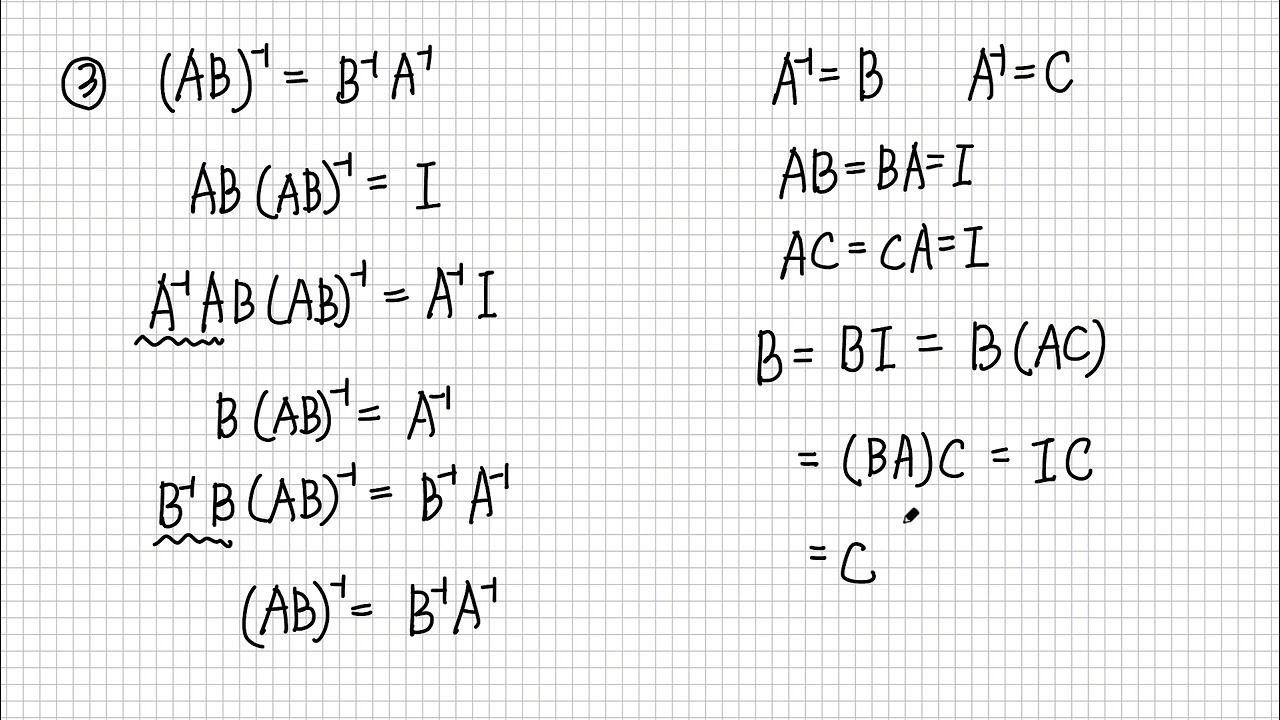
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 아핀 공간의 구성 요소 (0) | 2023.04.15 |
|---|---|
| 아핀 공간(Affine space) (0) | 2023.04.14 |
| 행렬의 설계 (0) | 2023.04.12 |
| 행렬 (0) | 2023.04.11 |
| 선형성과 선형 변환 (0) | 2023.04.10 |
