이득우의 게임 수학
2차원 좌표계에서 원점을 지나는 직선은 선형성(Linearity)을 갖는다.
선형성을 갖는 함수는 다음 두 가지를 만족해야 한다.
1. 가법성(Superposition)
f(x1 + x2) = f(x1) + f(x2)
2. 1차 동차성(Homogeneity)
f(k·x) = k·f(x)



이차 함수는 선형성을 갖지 않는다.
- f(x1 + x2) = x1² + x2² + 2·x1·x2
- f(x1) + f(x2) = x1² + x2²

일차 함수라고 하더라도, 원점을 지나지 않는다면 선형성을 갖지 않는다.
- f(x1 + x2) = a·(x1 + x2) + b
- f(x1) + f(x2) = a·x1 + a·x2 + 2·b
선형성은 단지 곧게 뻗은 성질이 아니라, 두 집합의 순수한 비로 구성된 1차적 대응 관계를 의미한다.

2차원 벡터를 입력 받아 2차원 벡터를 출력하는 f(v) = f(x, y) = (ax + by, cx + dy)라는 함수가 있다고 해보자.
- 계산해보면 이 함수는 가법성과 1차 동차성을 만족하므로, 선형성을 갖고 있다고 할 수 있다.
표준 기저 벡터(e1, e1, ..)의 선형 결합으로 형성된 벡터 공간은 선형성을 지니고, 이 공간을 선형 함수로 변화시킨 새 공간도 기저 벡터의 선형 결합으로 표현되므로 선형성을 지닌다.
이렇게 두 공간이 동일한 구조를 지닐 때, 두 공간의 대응 관계를 변환(Transformation)이라고 하고, 선형성을 유지시켜주는 선형 함수 f(x, y) = (ax + by, cx + dy)를 특히, 선형 변환(Linear Transformation)이라고 한다.
- 선형 변환은 역함수를 통해, 변환 전의 벡터를 파악할 수 있다.

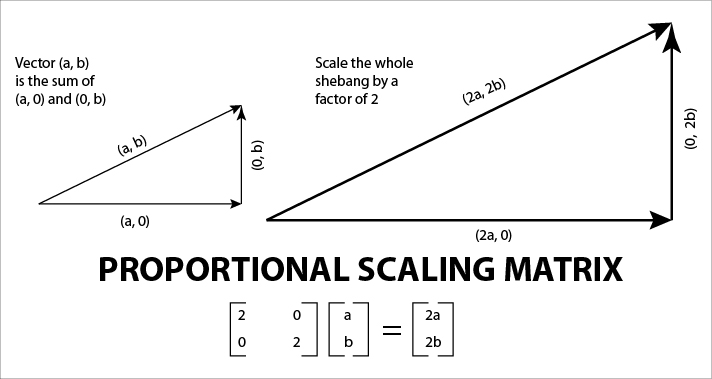
선형 함수 f(x, y) = (ax + by, cx + dy)에 각각 다음 값들을 대입하면 크기 변환과 회전 변환이 된다.
- 크기 변환 (a, b, c, d) = (k, 0, 0, k)
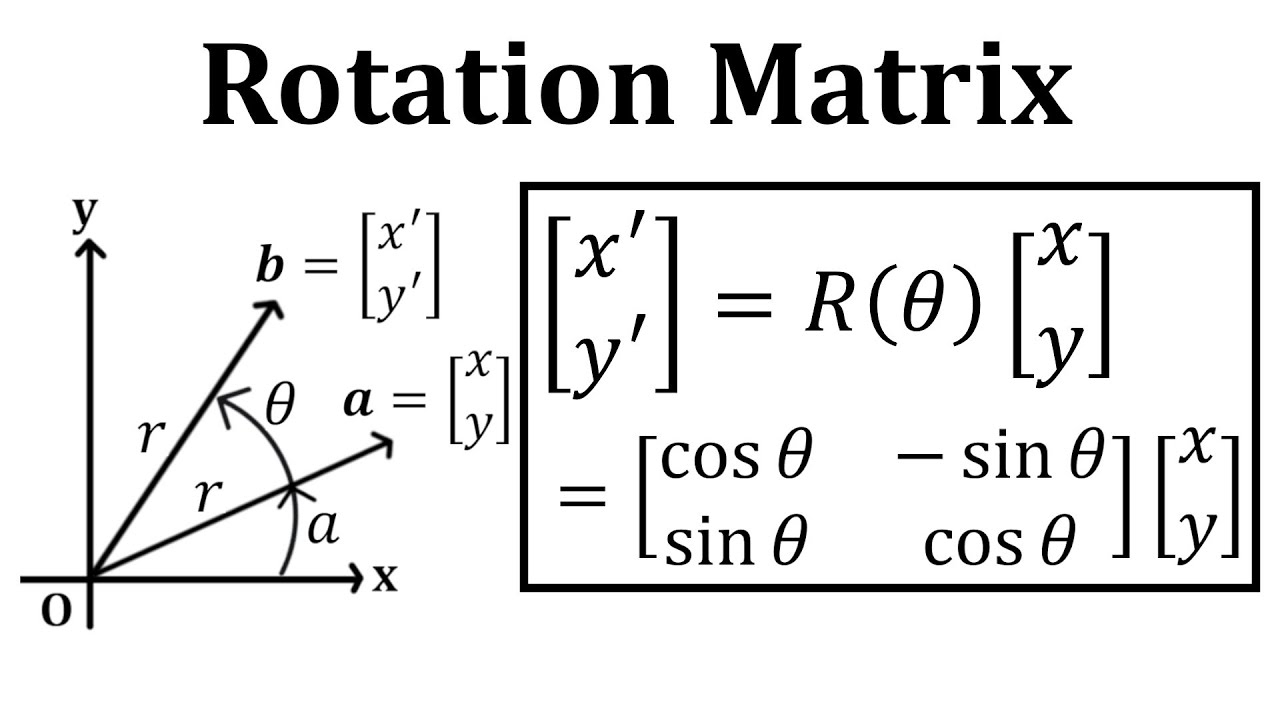
- 회전 변환 (a, b, c, d) = (cosθ, -sinθ, sinθ, cosθ)
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 행렬의 설계 (0) | 2023.04.12 |
|---|---|
| 행렬 (0) | 2023.04.11 |
| 극좌표계 (0) | 2023.04.09 |
| 삼각함수의 역함수 (0) | 2023.04.08 |
| 삼각함수를 활용한 벡터의 회전 (0) | 2023.04.08 |

