이득우의 게임 수학
벡터를 더하거나 늘리는 동작은 x축, y축이 서로 독립적으로 적용된다.
- 종속적이지 않고 각각 따로 계산해도 된다.
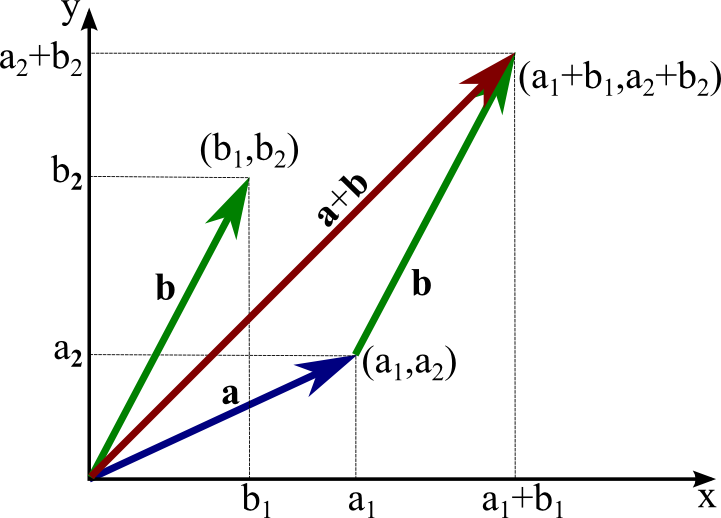
하지만 회전은 x, y 값이 서로 영향을 미치기 때문에, 독립적으로 계산할 수 없다.
실벡터 공간 R²의 표준 기저 벡터 e1 (1, 0), e2 (0, 1)를 이용해 공간에 있는 모든 벡터를 표현할 수 있다.
각각을 θ만큼 회전시킨 좌표는 다음과 같다.
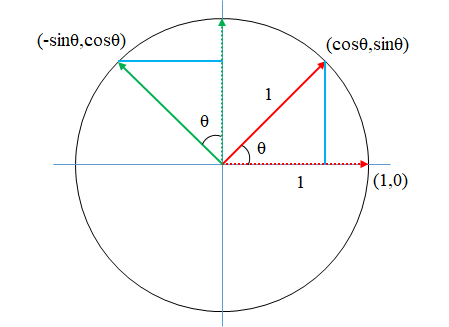
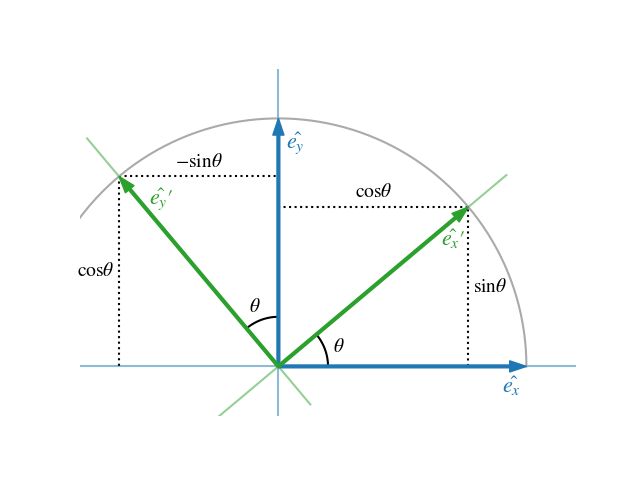
임의의 벡터 v (1, 1) = e1 (1, 0) + e2 (0, 1)를 θ만큼 회전시킨 v'의 좌표는 다음과 같다.
- (cosθ, sinθ) + (-sinθ, cosθ)
- (cosθ - sinθ, sinθ + cosθ)
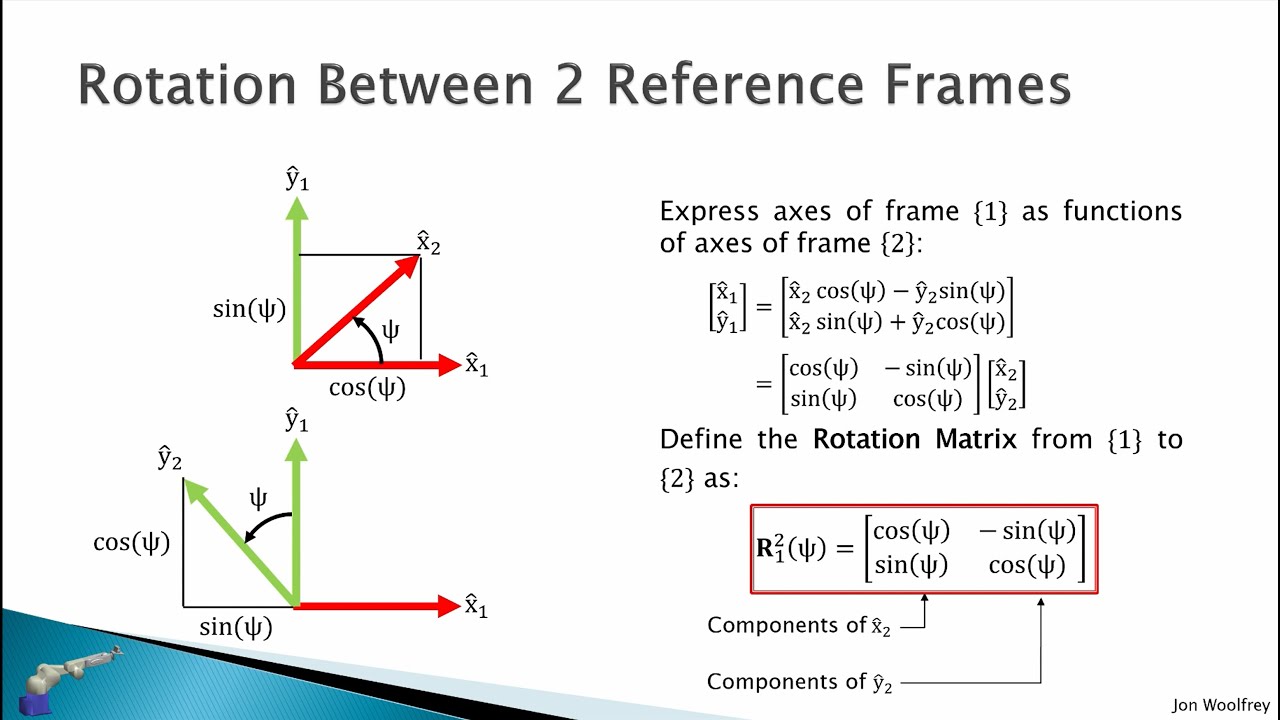
이와 같은 원리로, 벡터 u (x, y) = x·e1 + y·e2를 θ만큼 회전시킨 u'의 좌표는 다음과 같다.
- x·(cosθ, sinθ) + y·(-sinθ, cosθ)
- (xcosθ - ysinθ, xsinθ + ycosθ)
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 극좌표계 (0) | 2023.04.09 |
|---|---|
| 삼각함수의 역함수 (0) | 2023.04.08 |
| RGB와 HSV 색 공간 (0) | 2023.04.07 |
| 삼각함수 (0) | 2023.04.06 |
| 벡터의 결합과 기저 (0) | 2023.04.06 |

