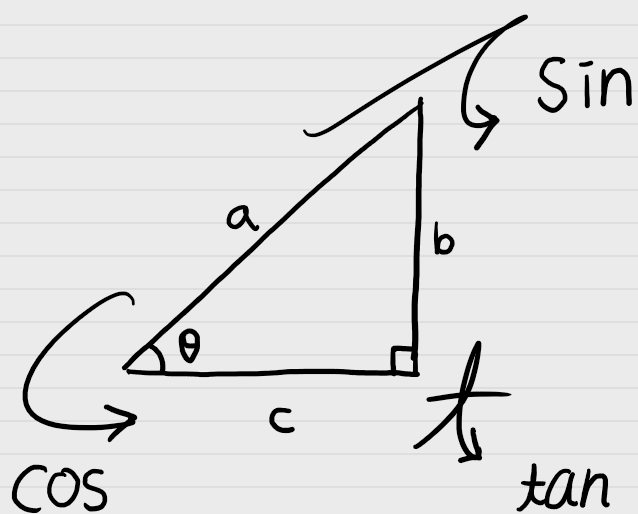
이득우의 게임 수학
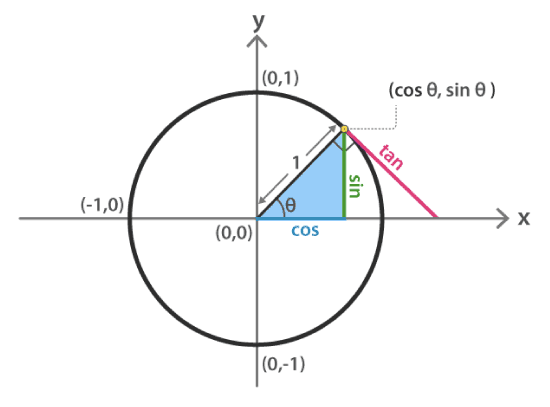
반지름의 길이가 1인 원에서 각이 θ일 때, 원주 위의 점 A의 좌표는 (cosθ, sinθ)이다.
- 반지름이 r이면, (r cosθ, r sinθ)이다.
이것을 피타고라스의 정리에 대입하면 cos²θ + sin²θ = 1이 된다.
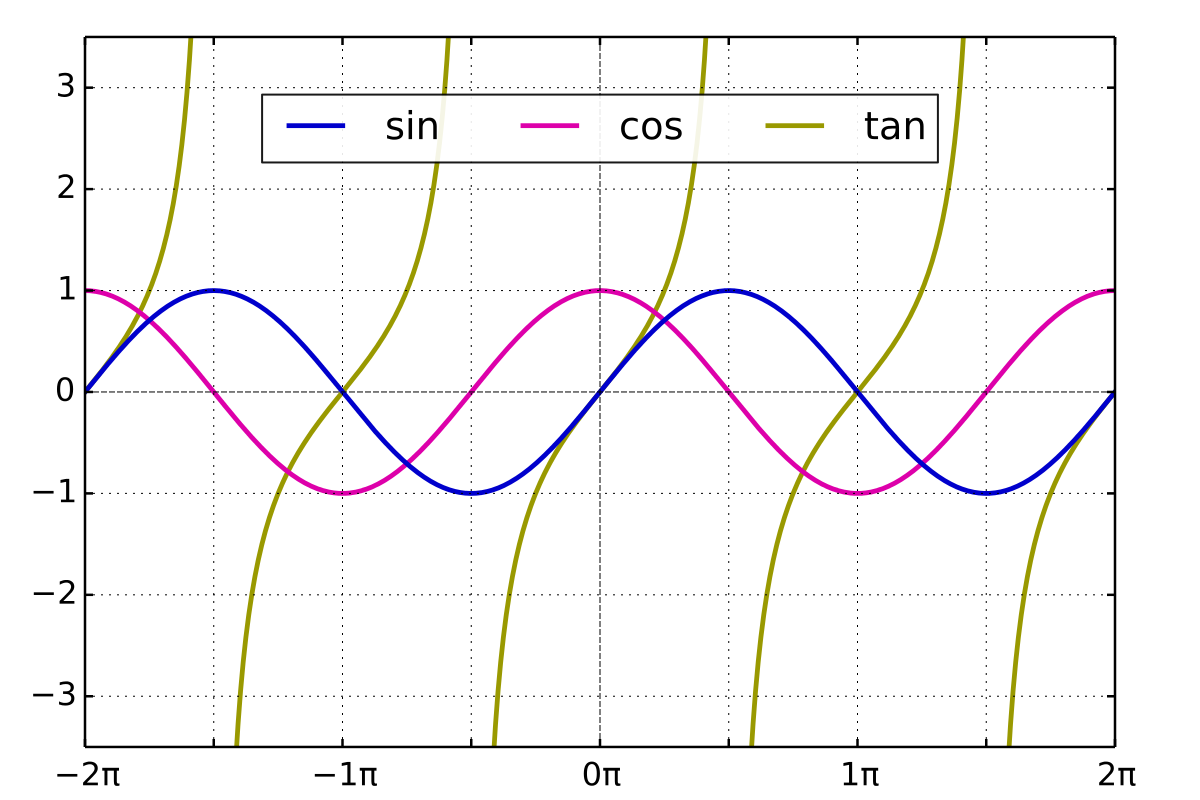
변화 값의 범위를 진폭(Amplitude)이라고 하고, 반복되는 각도를 주기(Period)라고 한다.
- sin, cos 함수는 다음과 같은 값을 갖는다.
진폭: 1
주기: 2π (360°)
마루(crest, peak): 1
골(trough): -1
cos 함수처럼 좌우 대칭인 함수를 짝함수(Even function)라고 하고, sin함수처럼 원점 대칭인 함수를 홀함수(Odd function)라고 한다.
- 짝함수이면, f(x) = f(-x)
- 홀함수이면, f(x) = -f(-x)
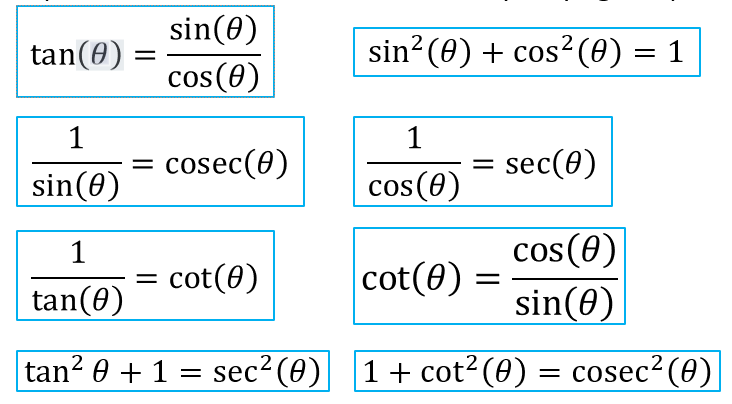
호도법
각을 측정할 때, 단위량 1을 기반으로 상대적인 크기를 측정한다.
각의 크기를 직접 측정하는 각도법 대신 호의 길이를 기준으로 각을 측정하는 방법이다.
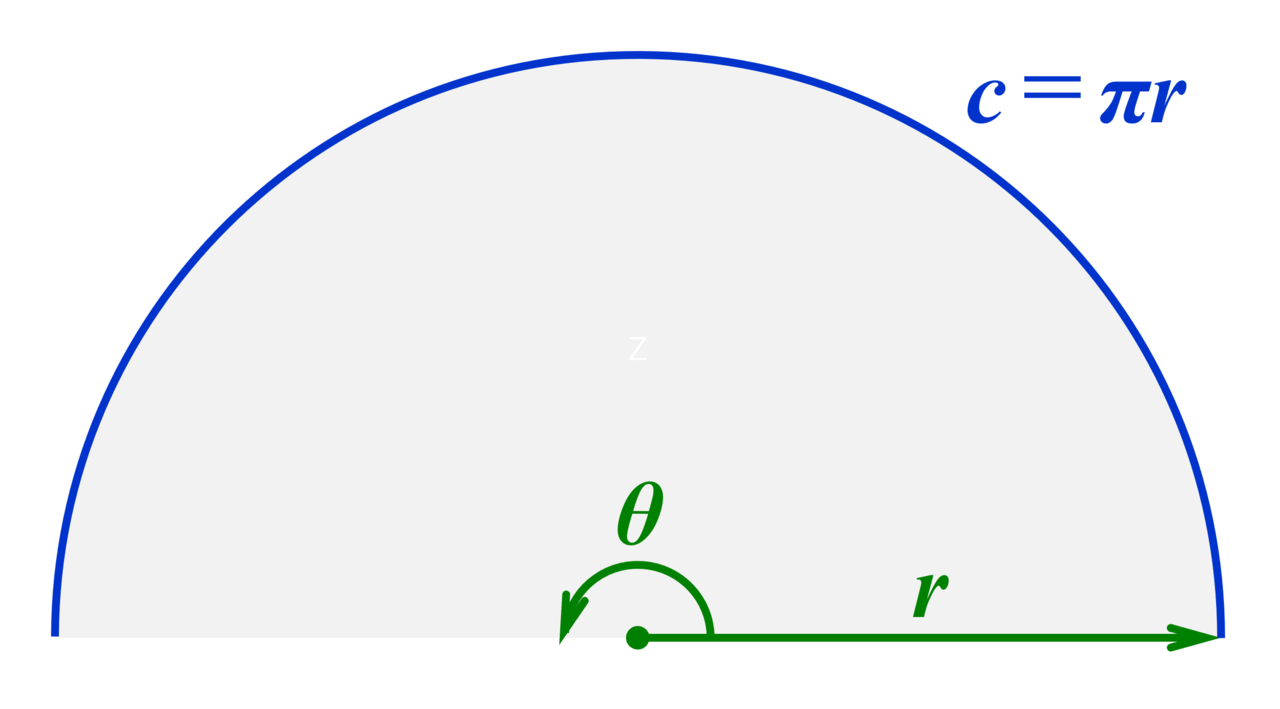
우리는 흔히 π = 180°라고 알고 있다.
- 호도법으로 길이가 1인 원의 둘레 절반의 길이가, 반지름의 약 3.14배인 π = 3.141592..이기 때문이다.
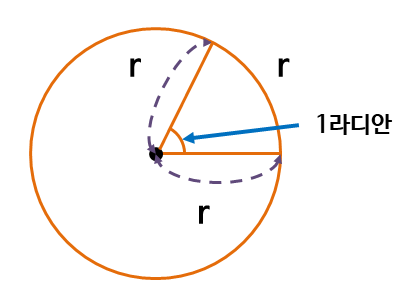
호도법으로 반지름이 1인 원에서 호의 길이가 1인 부채꼴의 중심각을 1 rad (radian, 라디안)이라고 하며, 약 52.2958°이다.
- 반지름이 1인 원에서, π rad = 180°이다.
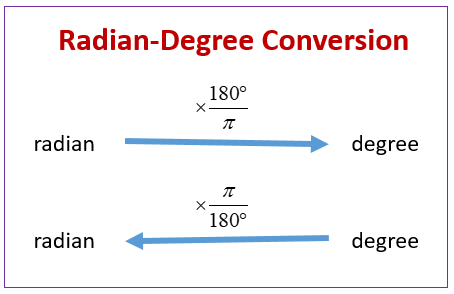
1 rad |
180 ㅡㅡㅡ ° π |
호의 길이가 1일 때 중심각 |
1° |
π ㅡㅡㅡ rad 180 |
중심각이 1°일 때 호의 길이 |
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 삼각함수를 활용한 벡터의 회전 (0) | 2023.04.08 |
|---|---|
| RGB와 HSV 색 공간 (0) | 2023.04.07 |
| 벡터의 결합과 기저 (0) | 2023.04.06 |
| 벡터(Vector) (0) | 2023.04.05 |
| 함수 (0) | 2023.04.04 |
