이득우의 게임 수학
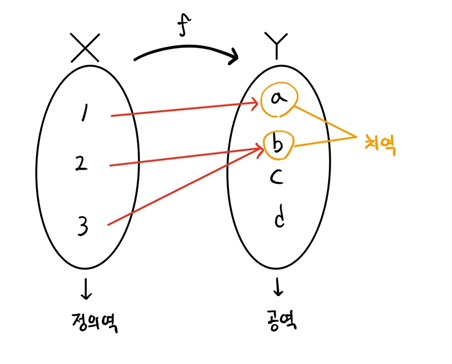
함수
- 정의역의 모든 원소는 공역의 원소에 대응되어야 한다.
- 하나의 정의역 원소는 하나의 공역 원소에만 대응되어야 한다.

프로그래밍 관점에서 정의역의 원소를 x, 대응하는 공역의 원소를 y라고 하면, 입력 x에 대해 출력 y = f(x)가 존재한다.

전사 함수
- 공역의 모든 요소가 정의역에 대응되는, 즉 공역과 치역이 같은 함수다.
단사 함수
- 정의역과 공역의 요소가 일대일로 대응되는 함수다.
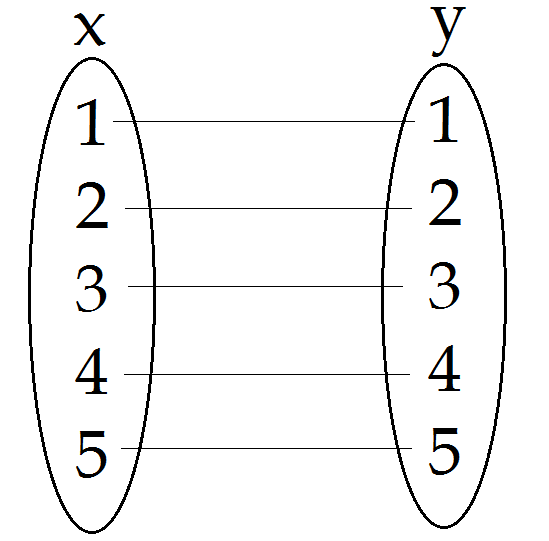
전단사 함수
- 정의역의 모든 원소와 공역의 모든 원소가 일대일로 대응되는 함수다.
- 역함수가 존재하기 위한 필요충분 조건이다.

합성 함수는 g º f = g(f(x))로 오른쪽에 있는 함수가 먼저 실행됨에 유의한다.
- h º (g º f) = (h º g) º f로 합성 함수는 결합 법칙이 성립한다.

정의역의 모든 원소에 대해, f(x) = x를 만족하면 항등 함수다.
함수 f에 대해, h º f = 항등 함수를 만족하면 h는 f의 역함수다.
- 역함수는 대응 관계를 뒤집어, 공역에서 정의역에 대응하는 함수로도 볼 수 있다.
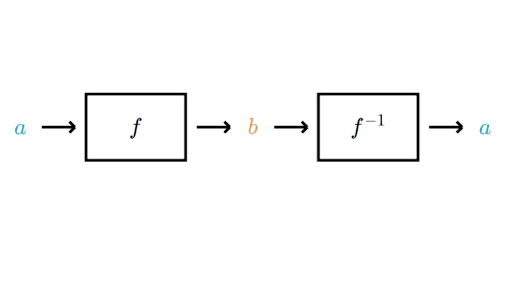
역함수는 다음의 성질을 만족한다.

'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| RGB와 HSV 색 공간 (0) | 2023.04.07 |
|---|---|
| 삼각함수 (0) | 2023.04.06 |
| 벡터의 결합과 기저 (0) | 2023.04.06 |
| 벡터(Vector) (0) | 2023.04.05 |
| 수와 집합 (0) | 2023.04.04 |