이득우의 게임 수학
선형 결합의 결과가 영벡터가 되는 유일한 해가 모든 스칼라가 0인 경우면 선형 독립, 그렇지 않으면 선형 종속이다.

모든 스칼라가 0이 아닌 해가 존재하는 선형 종속은, 적어도 하나의 벡터를 나머지 벡터로 표현할 수 있다는 뜻이다.
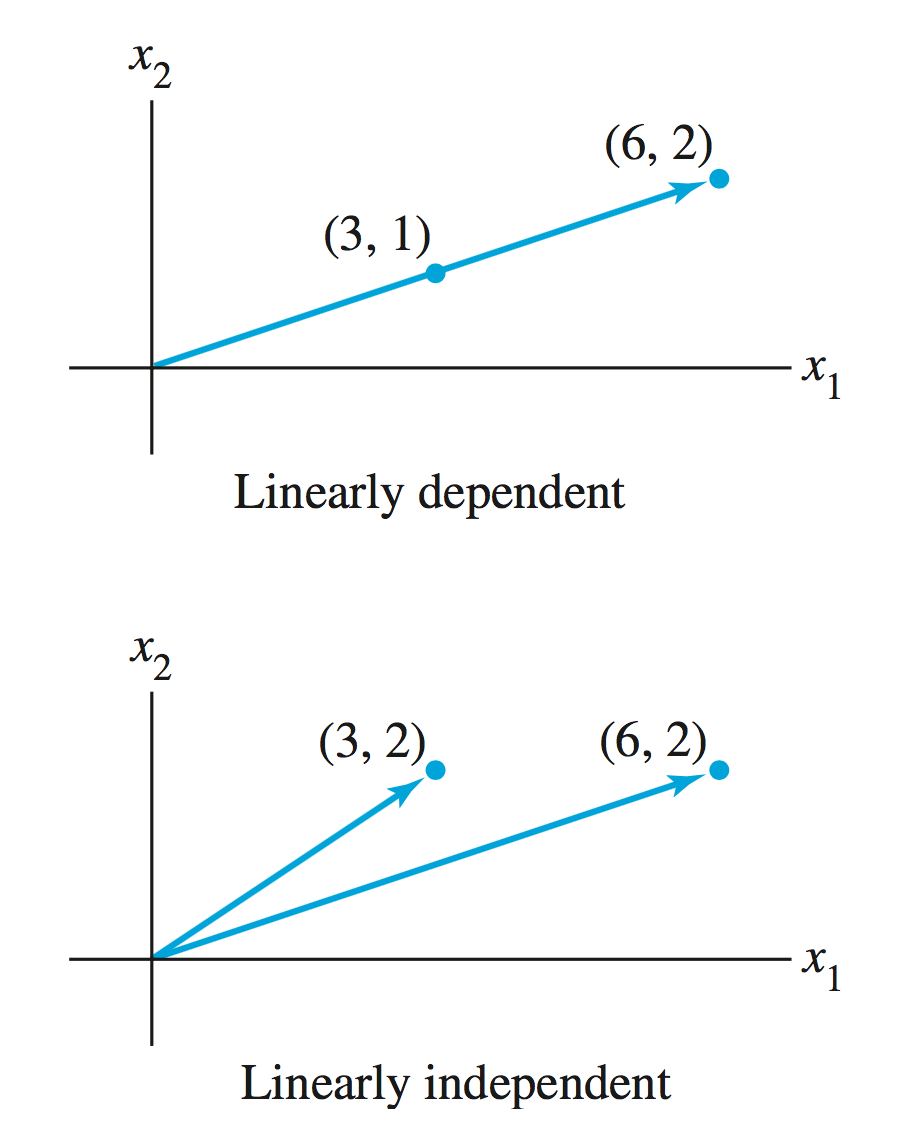
두 벡터 (3, 2), (6, 2)와 같이 벡터 공간 내 모든 벡터를 생성할 수 있는 선형 독립 관계를 갖는 벡터의 집합을 기저(Basis)라고 한다.
- (1, 0)은 기저 B = {(1, 0), (0, 1)}에 속한 기저 벡터이다.
- (6, 2)는 기저 B = {(3, 2), (6, 2)}에 속한 기저 벡터이다.
공간을 구성하는 다양한 기저 중 단위 벡터로만 구성된 집한을 특별히, 표준 기저(Standard basis)라고 한다.
- 기저 B = {(1, 0, 0), (0, 1, 0), (0, 0, 1)}은 공간 3차원 실벡터 공간(Real vector space) R³의 표준 기저다.
- 표준 기저는 다음과 같이 표현한다.
B = {e1, e2, e3, ...}
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| RGB와 HSV 색 공간 (0) | 2023.04.07 |
|---|---|
| 삼각함수 (0) | 2023.04.06 |
| 벡터(Vector) (0) | 2023.04.05 |
| 함수 (0) | 2023.04.04 |
| 수와 집합 (0) | 2023.04.04 |
