이득우의 게임 수학
역함수가 존재하기 위해서는 정의역의 모든 원소와 공역의 모든 원소가 일대일로 대응되는 전단사 함수여야 한다.
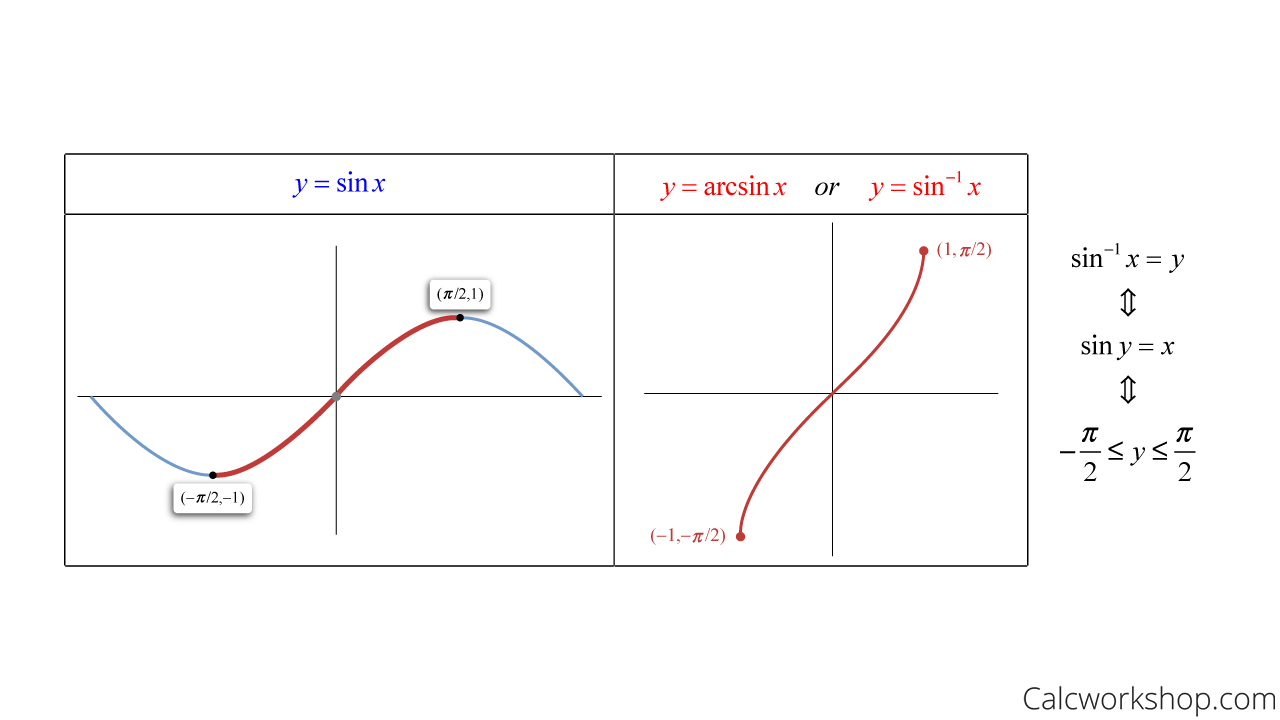
따라서 sin 함수의 경우, 범위를 [-90°, 90°] 구간으로 정의역의 범위를 제한해야 한다.
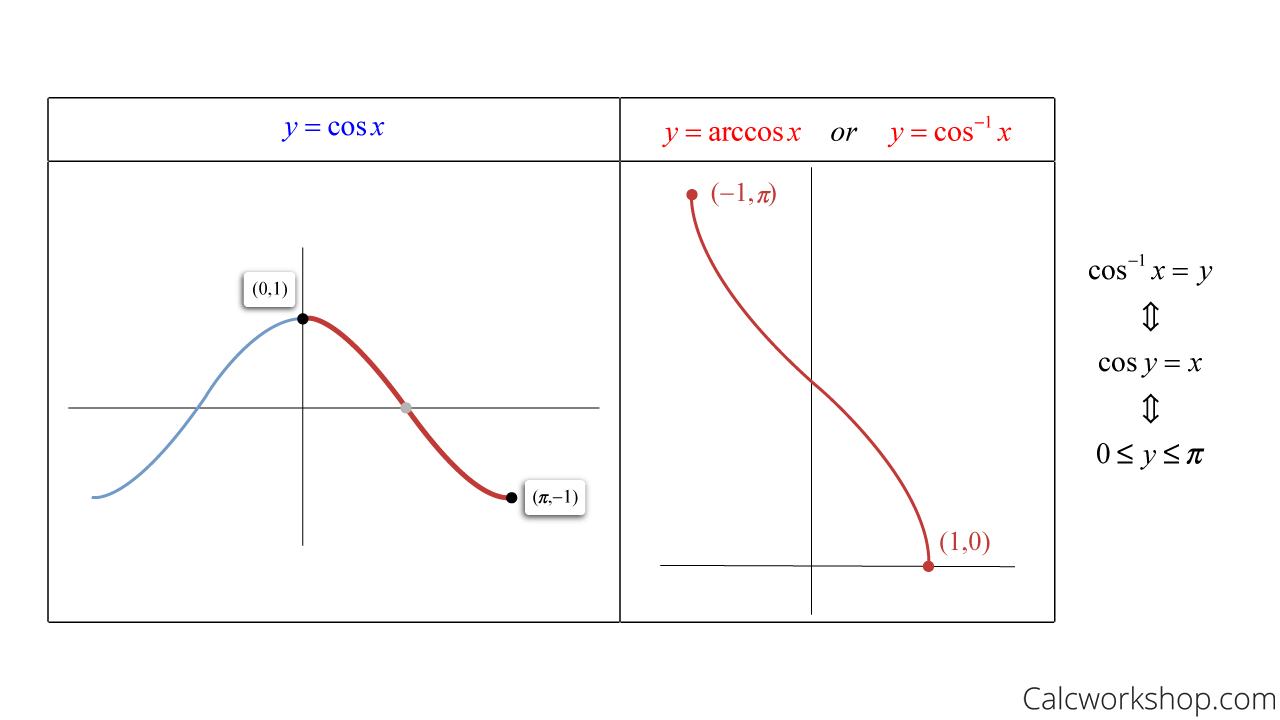
cos 함수의 경우, 범위를 [0°, 180°] 구간으로 정의역의 범위를 제한해야 한다.
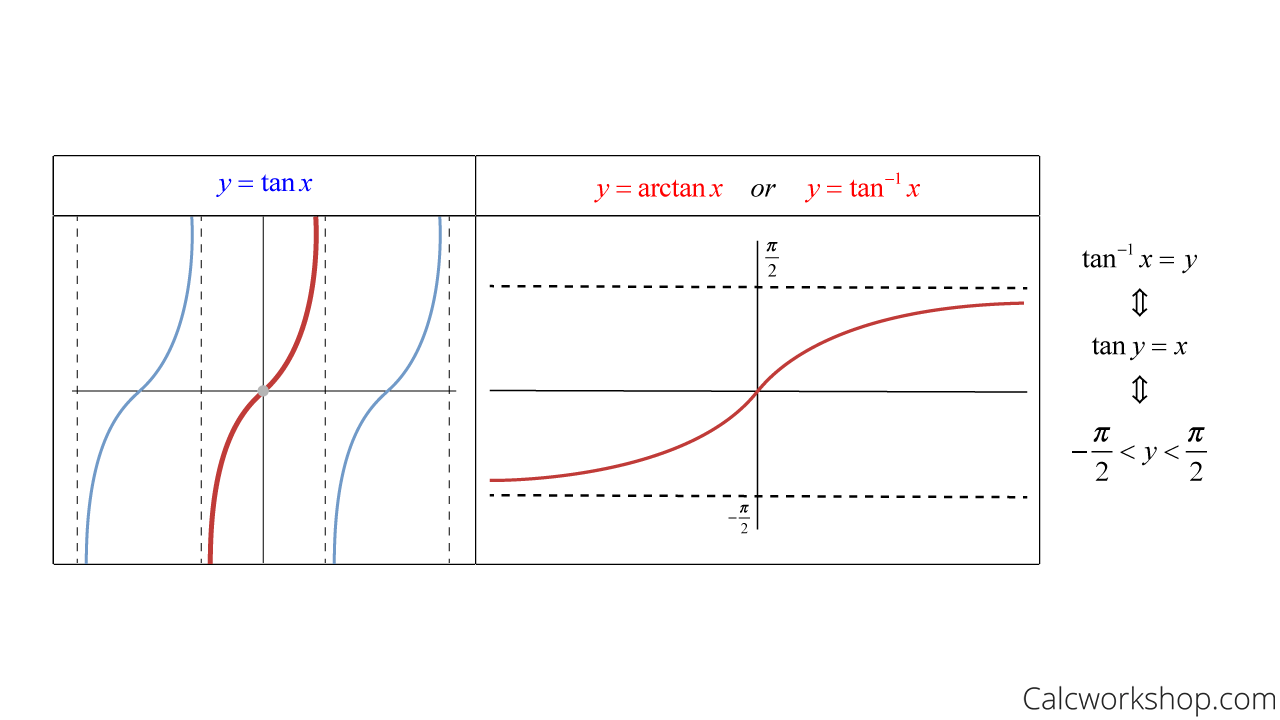
tan 함수의 경우, 범위를 (-90°, 90°) 구간으로 정의역의 범위를 제한해야 한다.
- tan 함수는 θ가 -90°, 90°일 때 y값이 존재하지 않기 때문에 제외해야 한다.
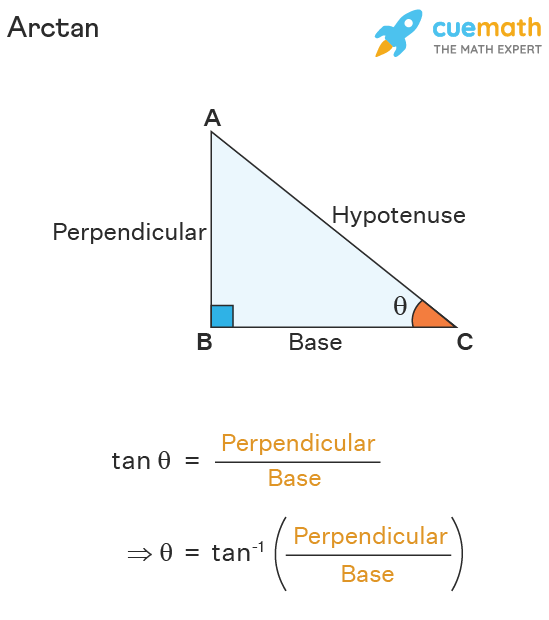
tanθ = y / x이기 때문에, arctan 함수를 활용하면 벡터의 각도를 알 수 있다.
- θ = arctan(y / x)
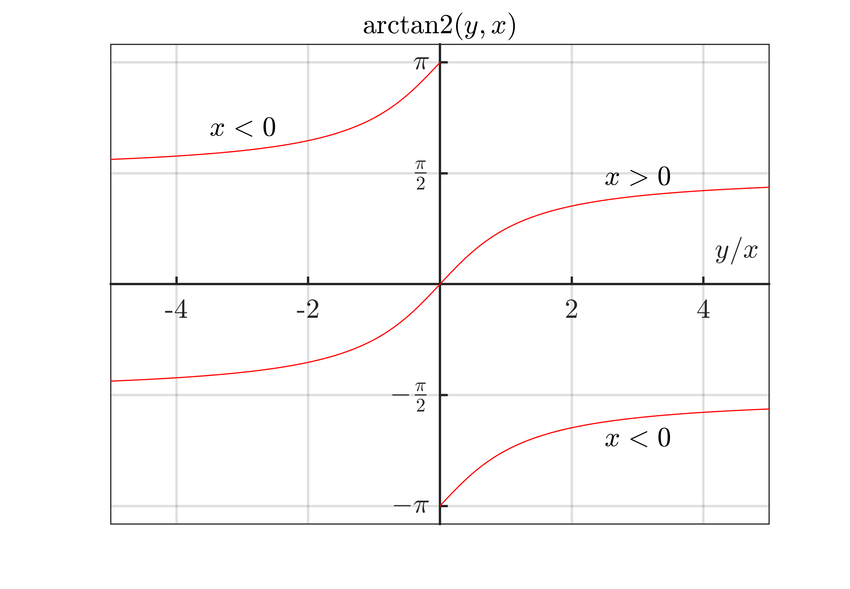
그런데 이때, y / x의 값을 분수로 전달하기 때문에 사분면을 판별할 때 문제가 발생한다.
- v = (1, 1)일 때 y / x = 1, u = (-1, -1)일 때도, y / x = 1로 같기 때문이다.
그래서 arctan 함수에 y와 x값을 따로 전달해 사분면을 판별할 수 있게 하는 atan2 함수가 별도로 존재한다.
- atan2(y, x)와 같이 전달하면, 부호에 따라 사분면을 판별할 수 있다.
- (-180°, 180°) 구간을 공역으로 갖는다.
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 선형성과 선형 변환 (0) | 2023.04.10 |
|---|---|
| 극좌표계 (0) | 2023.04.09 |
| 삼각함수를 활용한 벡터의 회전 (0) | 2023.04.08 |
| RGB와 HSV 색 공간 (0) | 2023.04.07 |
| 삼각함수 (0) | 2023.04.06 |
