이득우의 게임 수학
브레젠험 알고리즘은 시작점에서 끝점까지 한 픽셀씩 전진하면서 점을 찍기 때문에, 스크린을 벗어나는 굉장히 큰 값이 들어올 때도 마찬가지로 진행해야 한다.
따라서, 스크린 영역을 벗어나는 선분이 들어와도 영역에 유효한 선분으로 잘라주는 클리핑(Clipping) 작업이 필요하다.
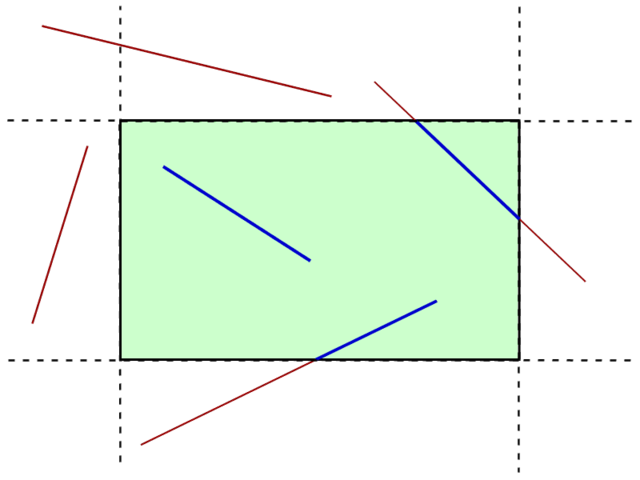
코헨-서덜랜드 라인 클리핑 알고리즘(Cohen-Sutherland Line Clipping Algorithm)
가운데 유효한 스크린 영역과 바깥 영역을 포함해 총 9개 영역으로 나눈 후, 두 점이 포함된 영역의 비트 연산을 통해 선분을 그려야 하는지 판별하고 클리핑을 진행하는 알고리즘이다.
위(10) / 중간(00) / 아래(01) + 왼쪽(01) / 중앙(00) / 오른쪽(10)
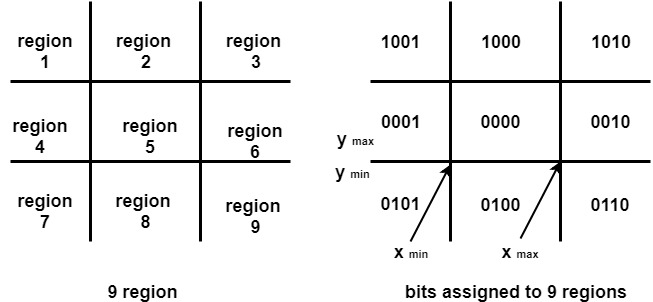
9개 중 어느 영역에 포함된 점인지 반환하는 함수는 다음과 같다.
- <이득우의 게임 수학> 도서의 예제 코드이다.
int WindowsRSI::TestRegion(const Vector2& InVectorPos, const Vector2& InMinPos, const Vector2& InMaxPos)
{
int result = 0;
if (InVectorPos.X < InMinPos.X)
{
result = result | 0b0001;
}
else if (InVectorPos.X > InMaxPos.X)
{
result = result | 0b0010;
}
if (InVectorPos.Y < InMinPos.Y)
{
result = result | 0b0100;
}
else if (InVectorPos.Y > InMaxPos.Y)
{
result = result | 0b1000;
}
return result;
}
시작과 끝점이 모두 0000 영역에 있다면 클리핑 없이 바로 선을 그리면 된다.
- 하지만, 한 점이라도 0000 밖에 위치한다면 클리핑을 진행해야 한다.

아래와 같이 두 점이 모두 0000 밖에 위치하는 경우에도 클리핑을 진행해야 하지만, 만약 선분이 스크린 영역을 전혀 지나지 않는다면 그릴 필요가 없다.
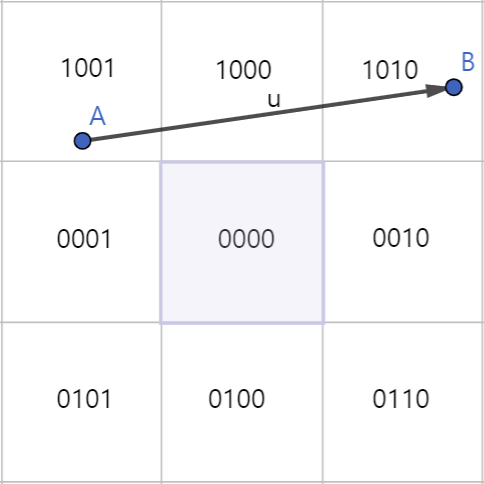
따라서, 총 3가지 경우가 존재한다.
1. 화면 안에 위치해서 자를 필요가 없다.
2. 화면 밖에 위치해서 그릴 필요가 없다.
3. 화면을 가로질러서 잘라내야 한다.
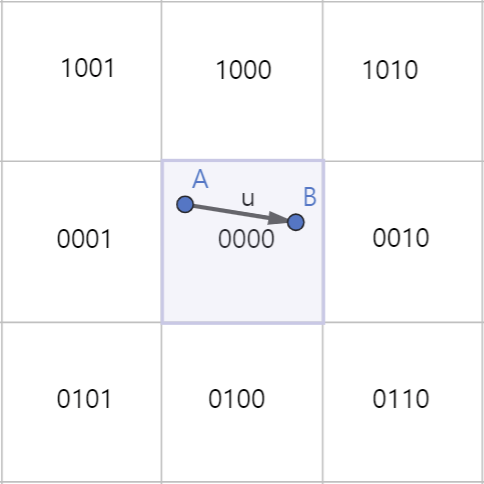
상황 1은 두 점의 값이 모두 0000이고 그냥 그리면 된다.
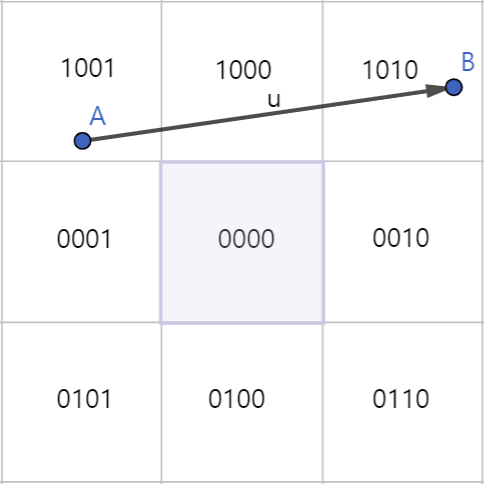
선분이 스크린 밖에 있어 그릴 필요가 없는 상황 2는, 두 점이 중앙이 아닌 동일한 가로 혹은 세로 영역에 있는 경우이다.
- 이때는 상하/좌우 중 최소 1개 이상이 같기 때문에, & 연산의 값이 항상 0보다 크게 나온다.
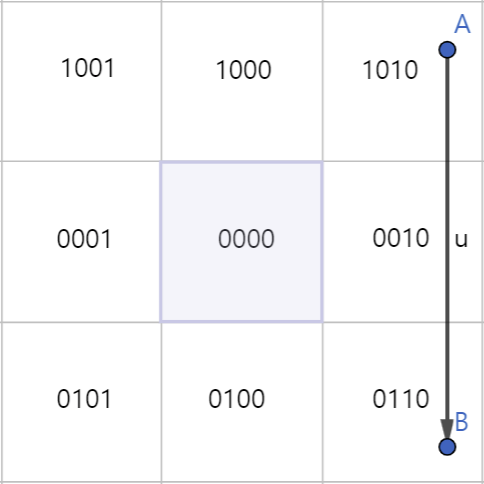
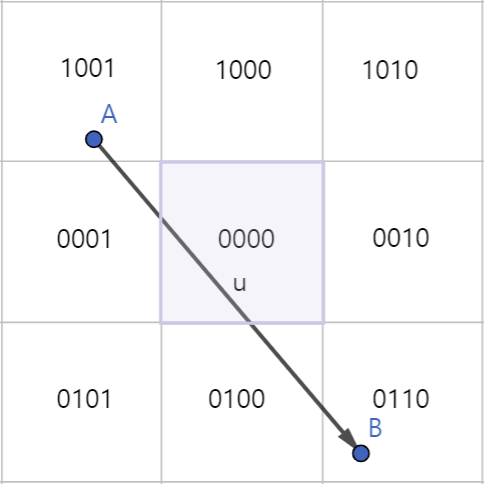
두 점이 대각선인 영역에 위치해 선분을 잘라내야 하는 경우에는 & 연산의 값이 항상 0이 나온다.
- 상하/좌우가 모두 다르기 때문이다.
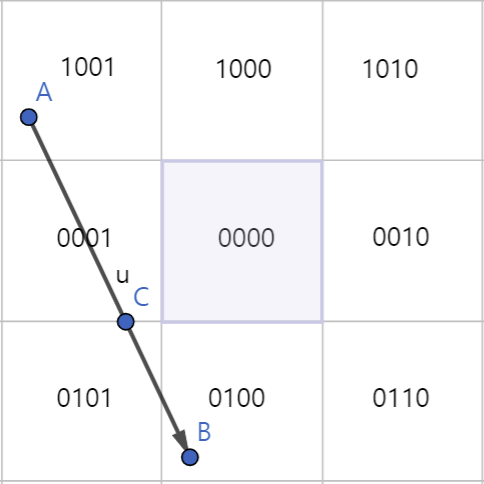
- 한 점씩 클리핑해 스크린 영역으로 이동시키고 두 점의 값이 모두 0000이 되면 그리면 된다.
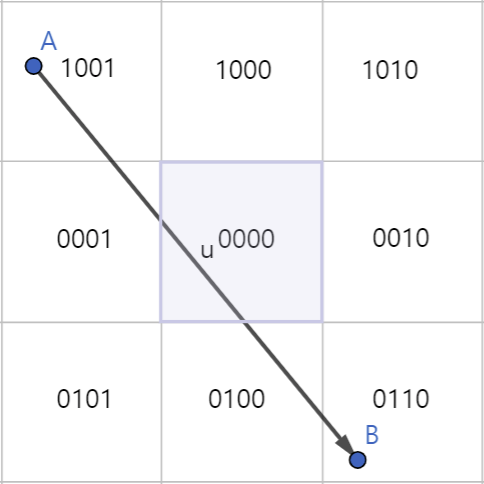
그런데 이때 좌측과 같이 클리핑을 진행해야 하는 경우도 있고, 우측과 같이 그릴 필요가 없는 경우도 있다.
- 우측의 경우 한 점을 클리핑한 후, 다시 영역 테스트를 진행하면 & 연산의 결과가 상황 1에 해당하는 0보다 큰 값이 나오므로 그리지 않아도 되게 된다.
C++ 코드로 코헨-서덜랜드 알고리즘을 구현하면 다음과 같다.
- <이득우의 게임 수학> 도서의 예제 코드이다.
bool WindowsRSI::CohenSutherlandLineClip(Vector2& InOutStartPos, Vector2& InOutEndPos, const Vector2& InMinPos, const Vector2& InMaxPos)
{
int startTest = TestRegion(InOutStartPos, InMinPos, InMaxPos);
int endTest = TestRegion(InOutEndPos, InMinPos, InMaxPos);
float width = (InOutEndPos.X - InOutStartPos.X);
float height = (InOutEndPos.Y - InOutStartPos.Y);
while (true)
{
if ((startTest == 0) && (endTest == 0)) // 화면 안에 두 점이 있으면 바로 그리기
{
return true;
}
else if (startTest & endTest) // 화면 밖에 선이 있으므로 그릴 필요가 없음
{
return false;
}
else // 양쪽을 조사해 직선의 방정식을 이용해 클리핑을 진행
{
Vector2 clippedPosition;
bool isStartTest = (startTest != 0);
int currentTest = isStartTest ? startTest : endTest;
if (currentTest < 0b0100)
{
if (currentTest & 1)
clippedPosition.X = InMinPos.X;
else
clippedPosition.X = InMaxPos.X;
if (Math::EqualsInTolerance(height, 0.0f))
clippedPosition.Y = InOutStartPos.Y;
else
clippedPosition.Y = InOutStartPos.Y + height * (clippedPosition.X - InOutStartPos.X) / width;
}
else
{
if (currentTest & 0b0100)
clippedPosition.Y = InMinPos.Y;
else
clippedPosition.Y = InMaxPos.Y;
if (Math::EqualsInTolerance(width, 0.0f))
clippedPosition.X = InOutStartPos.X;
else
clippedPosition.X = InOutStartPos.X + width * (clippedPosition.Y - InOutStartPos.Y) / height;
}
// 클리핑한 결과로 다시 테스트 진행.
if (isStartTest)
{
InOutStartPos = clippedPosition;
startTest = TestRegion(InOutStartPos, InMinPos, InMaxPos);
}
else
{
InOutEndPos = clippedPosition;
endTest = TestRegion(InOutEndPos, InMinPos, InMaxPos);
}
}
}
return true;
}'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 내적을 활용한 시야 판별 (0) | 2023.04.21 |
|---|---|
| 내적(Dot product) (0) | 2023.04.20 |
| 브레젠험 알고리즘(Bresenham's algorithm) (0) | 2023.04.18 |
| 스크린 좌표계(Screen coordinate system) (0) | 2023.04.17 |
| 아핀 결합(Affine Combination) (0) | 2023.04.16 |
