이득우의 게임 수학
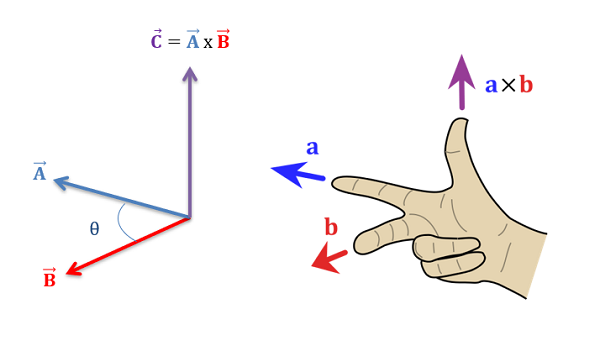
벡터 A와 벡터 B의 외적은 A⨯B로 나타낸다.
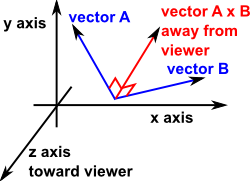
외적은 신발끈 공식(사선 공식)과 유사하게 아래와 같이 계산하고, 외적의 결과는 두 벡터에 동시에 수직인 벡터가 된다.
- 두 벡터로 만들어지는 평면의 법선 벡터(Normal Vector)를 만드는 것이다.


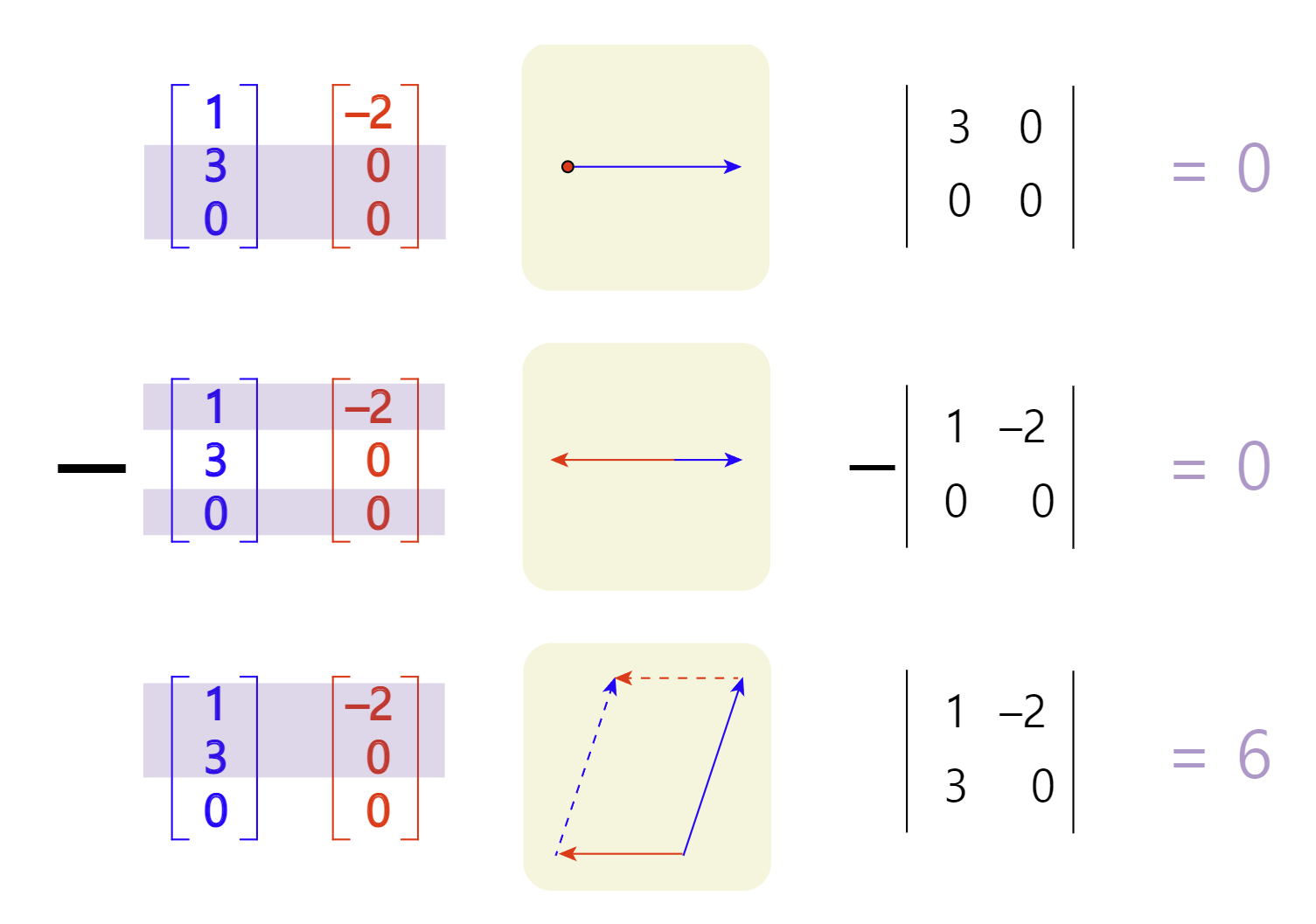
사실 외적의 결과가 되는 법선 벡터 C의 크기는 C의 행렬식의 절댓값과 같다.
- |A⨯B| = |det(C)|

외적은 연산 순서에 의해 크기는 바뀌지 않지만, 결과의 방향이 바뀐다.
- A⨯B = -(B⨯A)
- B⨯A = -A⨯B = A⨯-B = -B⨯-A

외적은 교환법칙과 결합법칙이 성립하지 않지만, 덧셈에 대한 분배법칙은 성립한다.
- A⨯B ≠ B⨯A
- C⨯(A⨯B) ≠ (C⨯A)⨯B
- C⨯(A + B) = C⨯A + C⨯B

외적의 크기는 두 벡터로 만들어지는 평행사변형의 넓이와 같다.
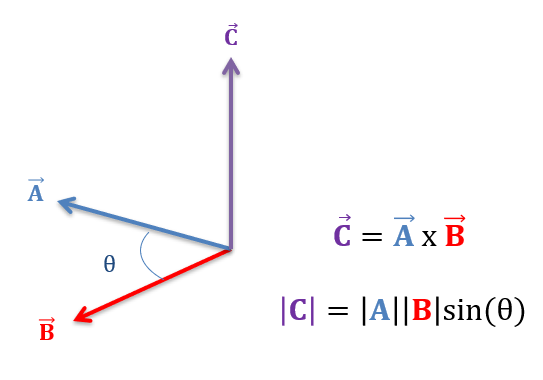
그러므로 직교성을 판별하는 내적과 달리, 외적은 두 벡터의 평행성을 판별하는 데 사용된다.
- sinθ는 두 벡터가 수직일 때 1, 사잇각이 0°와 180°일 때 0이다.
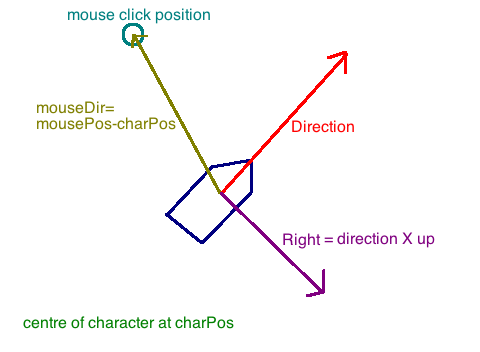
외적의 이런 성질을 활용하면, 게임에서 물체가 왼쪽에 있는지 오른쪽에 있는지 판별할 수 있다.
캐릭터의 시선 방향을 F, 캐릭터가 물체를 향하는 방향을 V, y축 위쪽 방향을 Y라고 하자.
물체가 벡터 F 기준 왼쪽에 있다면 F⨯V는 위쪽을 가리킬 것이고, 오른쪽에 있다면 아래쪽을 가리킬 것이다.
이때 Y와의 내적을 활용하면,
- (F⨯V)·Y > 0
물체가 캐릭터의 시선 기준 왼쪽에 있다. - (F⨯V)·Y < 0
물체가 캐릭터의 시선 기준 오른쪽에 있다. - (F⨯V) = 0
물체가 캐릭터의 시선 방향에 있다.
임의의 두 벡터에 직교하는 벡터를 생성하는 외적의 성질은 카메라의 회전을 설정하는 데도 사용된다.
임의의 벡터 V가 있을 때, V를 Local Z축으로 하는 새로운 Local 축을 구한다고 해보자.
Local X축은 Y⨯V로 구할 수 있고, Local Y축은 V⨯Local X로 구할 수 있다.
카메라의 로컬 축을 구했으니, 카메라 트랜스폼의 회전 행렬 R은 Local 축을 열 벡터로 지정해 다음과 같이 생성할 수 있다.

그러데, 고려해야 할 예외 상황이 몇 가지 있다.
1. 카메라의 위아래가 뒤집힌 경우
- 이때는 외적을 계산할 때 Y축 대신 -Y축을 사용해야 한다.
2. Local Z축이 Y(-Y)축과 일치하는 경우
- 이때는 외적의 값이 0이 되므로 더 이상 계산을 진행할 수 없기 때문에, Local X축을 수동으로 지정해줘야 한다.
일반적으로 카메라가 뒤집힐 경우는 없지만, 만약의 경우를 위해 외적에 사용될 UpVector(Y축)의 값을 입력받도록 설계하는 것이 안전하다.
<cpp />
// 책의 예제인 CK소프트렌더러에서 카메라의 방향을 재조정하는 함수
class CameraObject
{
public:
// 카메라 방향을 재조정하는 함수
void SetLookAtRotation(const Vector3& InTargetPosition, const Vector3& InUp = Vector3::UnitY)
{
Vector3 localX, localY, localZ;
// 로컬 Z축 생성
localZ = (InTargetPosition - _Transform.GetPosition()).GetNormalize();
// 시선 방향과 월드 Y축이 평행한 경우
if (Math::Abs(localZ.Y) >= (1.f - SMALL_NUMBER))
{
// 특이 상황에서 로컬 X 좌표 값을 임의로 지정.
localX = Vector3::UnitX;
}
else
{
localX = InUp.Cross(localZ).GetNormalize();
}
// 두 벡터가 직교하고 크기가 1이면 결과는 1을 보장
localY = localZ.Cross(localX);
_Transform.SetLocalAxes(localX, localY, localZ);
}
};
아래는 언리얼 엔진에서 입력으로 들어온 YAxis 벡터를 로컬 Y축으로 하는 새로운 축을 구축하는 함수이다.

'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 로드리게스 회전 공식 (0) | 2023.05.11 |
|---|---|
| 백페이스 컬링(Backface Culling) (0) | 2023.05.10 |
| 오일러 각에서의 회전 보간 (0) | 2023.05.08 |
| 짐벌 락(Gimbal Lock) (0) | 2023.05.07 |
| 카메라 공간 (0) | 2023.05.06 |