이득우의 게임 수학
오일러 각 방식은 짐벌락 현상이 발생하는 데다, 회전 순서에 따라 결과가 바뀌기 때문에 회전 보간이 어렵다.
이 문제는 임의의 축에 대한 평면의 회전 방식인 축-각 회전(Axis-Angle rotation)을 사용하면 해결이 가능하다.
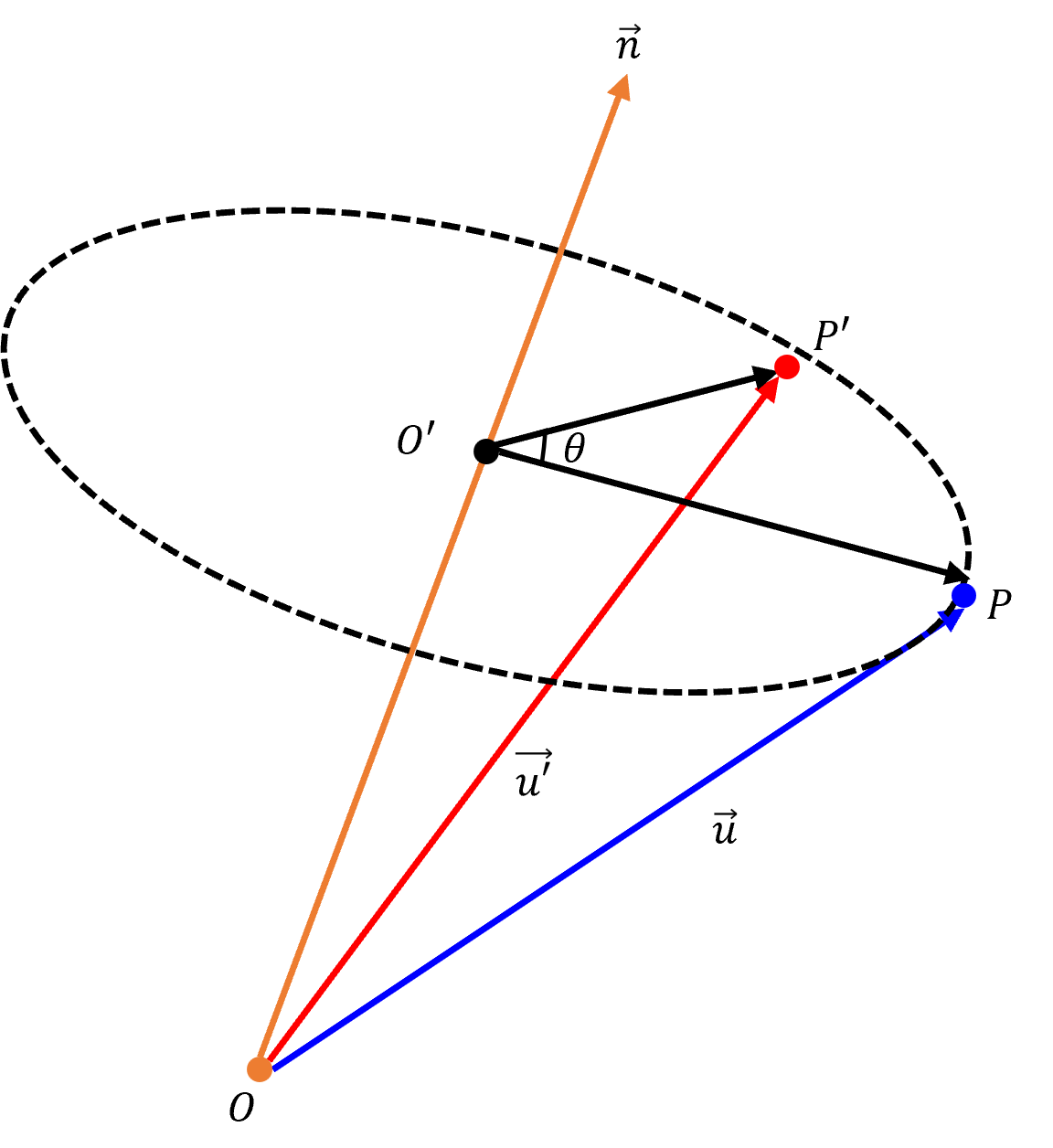
원점을 O(0, 0, 0, 1), 회전 평면의 중심을 O', 회전시킬 점을 P(x, y, z, 1), 회전한 점을 P'이라고 하자.
- 벡터 u = P - O = (x, y, z)가 된다.
벡터 u를 벡터 n에 투영(Projection)시킨 벡터를 v라고 할 때,
- 벡터 v = (u·nₑ)·nₑ
벡터 O'P = u - v가 된다.

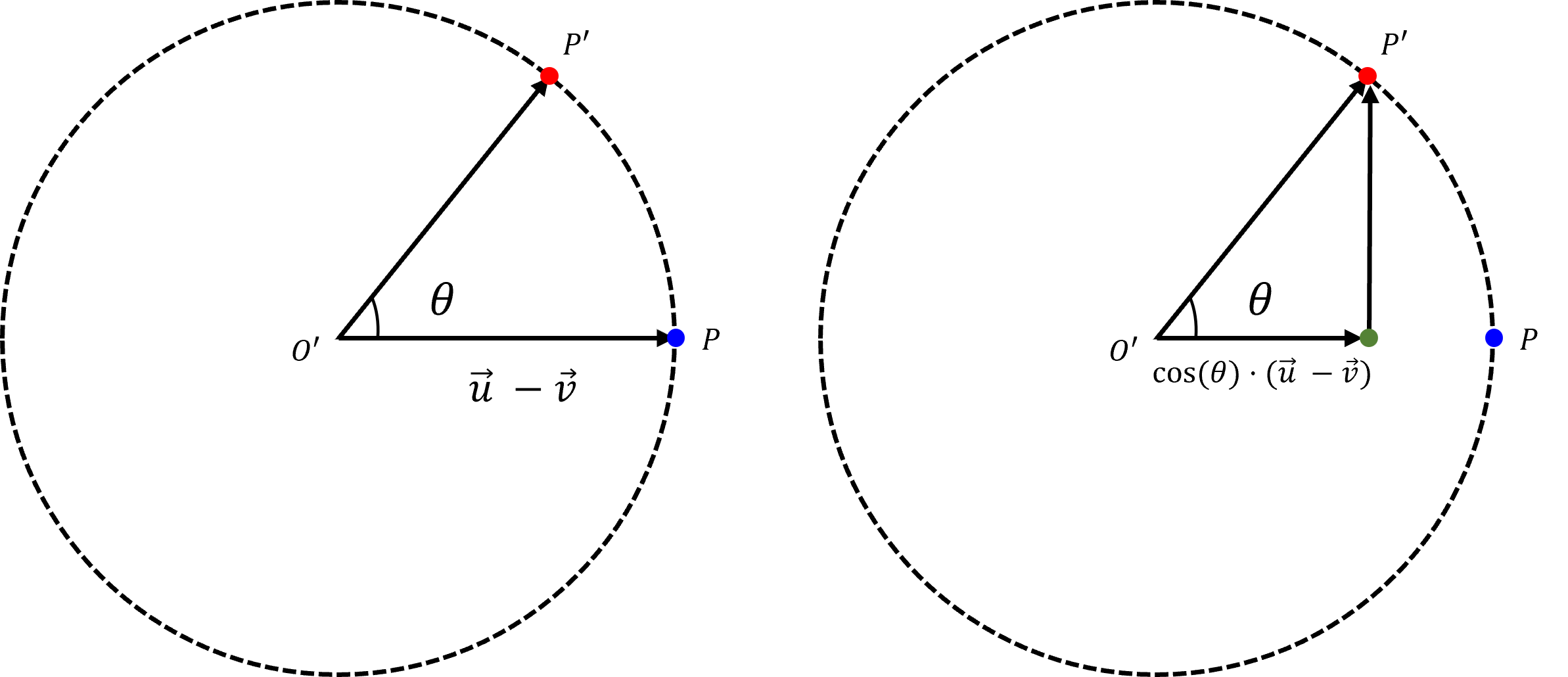
벡터 O'P'을 가로 성분과 세로 성분으로 분리하면, 가로 성분은 cosθ·(u - v)가 된다.
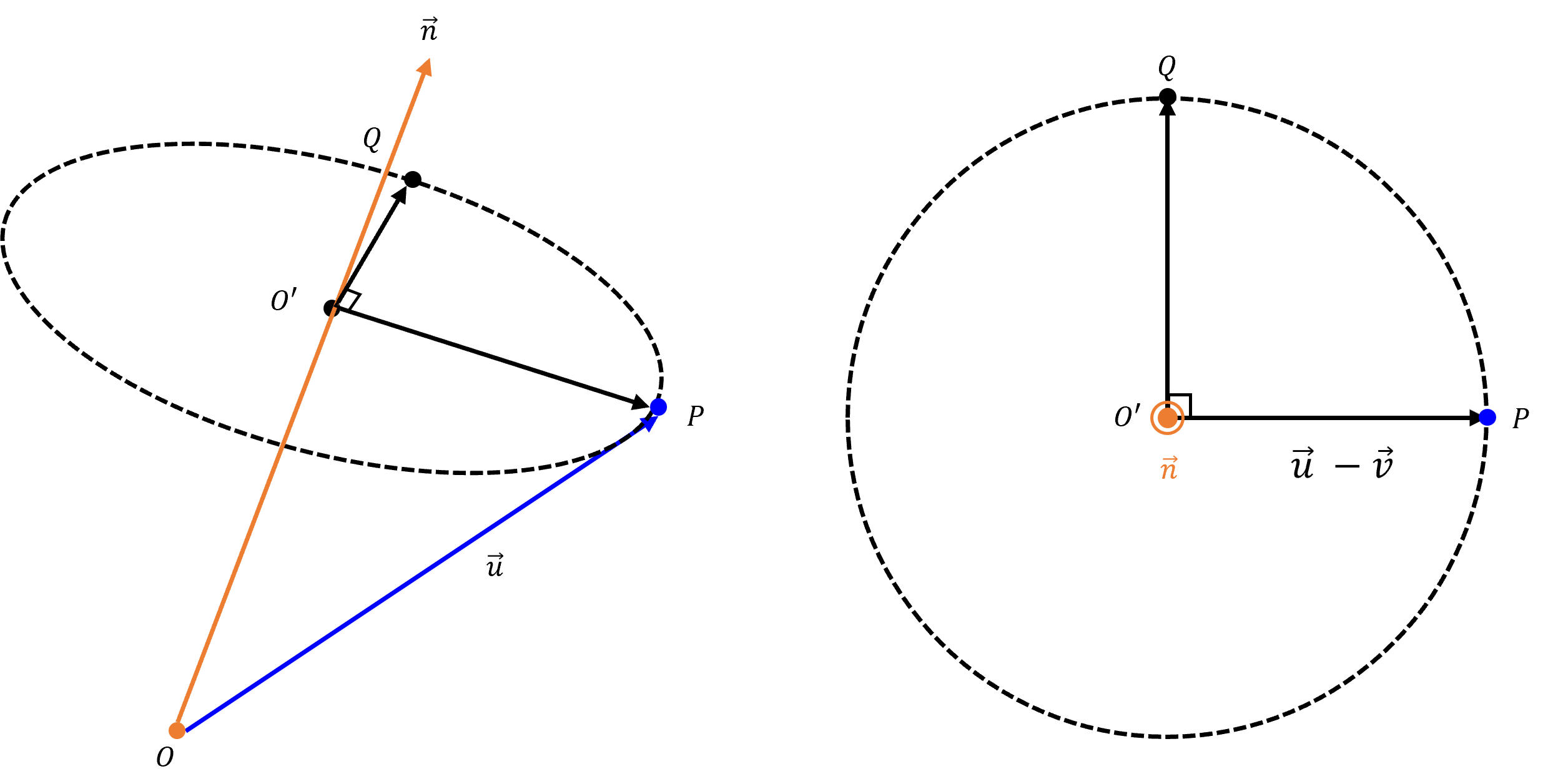
벡터 O'P'의 세로 성분을 구하기 위해서는 같은 방향을 향하는 벡터가 필요한데, 이는 nₑ와 O'P를 외적해 둘에 동시에 수직인 벡터 O'Q를 구할 수 있다.
- O'Q = nₑ⨯(u - v)가 된다.
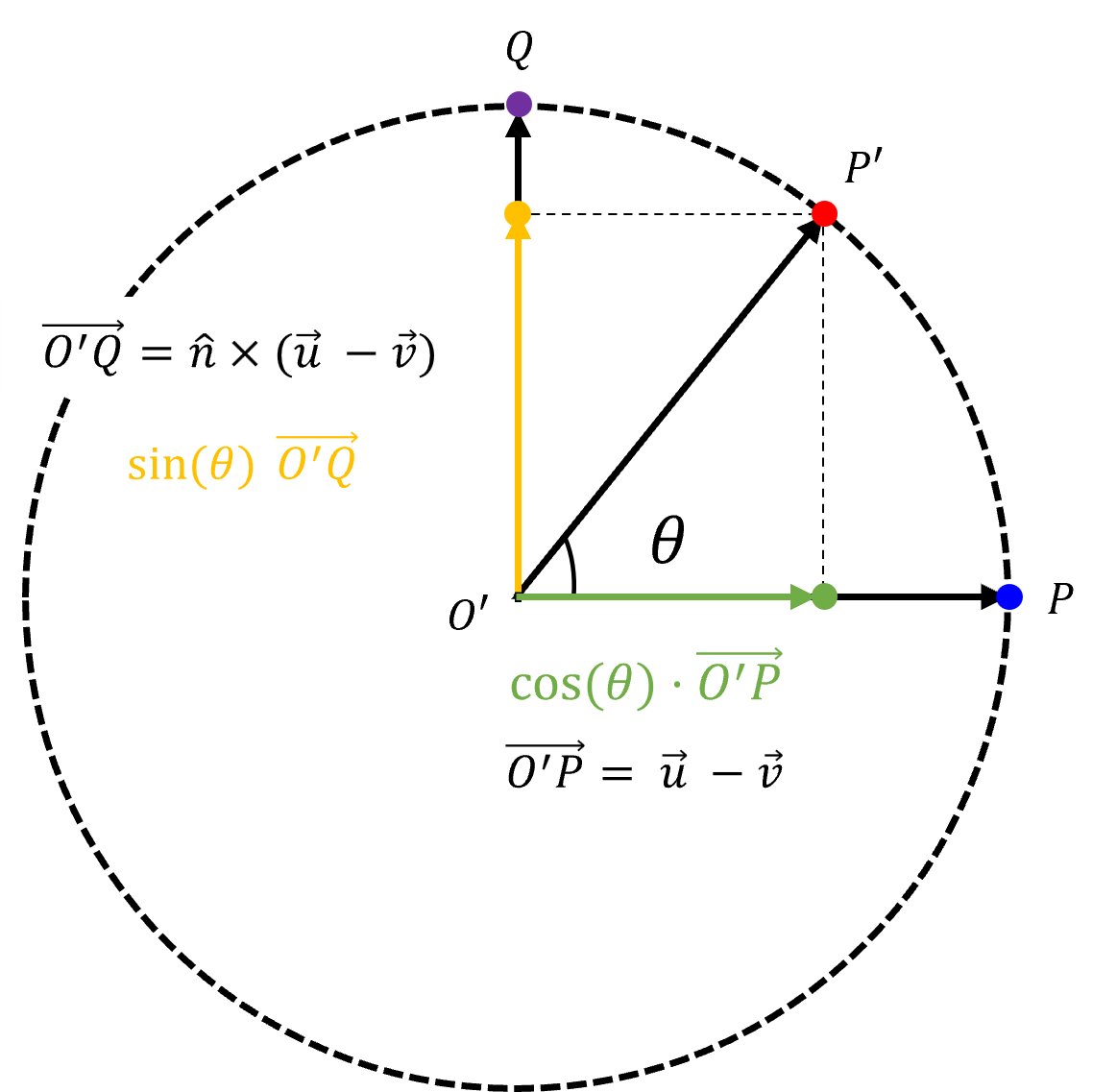
여기에 sinθ를 곱하면 세로 성분은 sinθ·(nₑ⨯(u - v))가 된다.
가로 성분과 세로 성분을 구했으니 두 벡터를 더하면 O'P'을 구할 수 있다.
O'P'
= cosθ·O'P + sinθ·O'Q
= cosθ·(u - v) + sinθ·(nₑ⨯(u - v))
= cosθ·(u - v) + sinθ·(nₑ⨯u - nₑ⨯v)
벡터 nₑ와 벡터 v는 평행하므로, 외적의 값은 항상 영벡터가 된다.
O'P' = cosθ·(u - v) + sinθ·(nₑ⨯u)
최종적으로 벡터 v를 (u·nₑ)·nₑ로 치환하면 벡터 OP'을 구할 수 있다.
이 공식을 로드리게스 회전 공식(Rodrigues' rotation formula)이라고 한다.
로드리게스 회전 공식을 활용하면 오일러 각으로 구현하기 어려운 임의 축에 대한 회전 변환을 수행할 수 있지만, 행렬로의 변환이 어렵다보니 렌더링 파이프라인에 연동하기가 까다롭다.
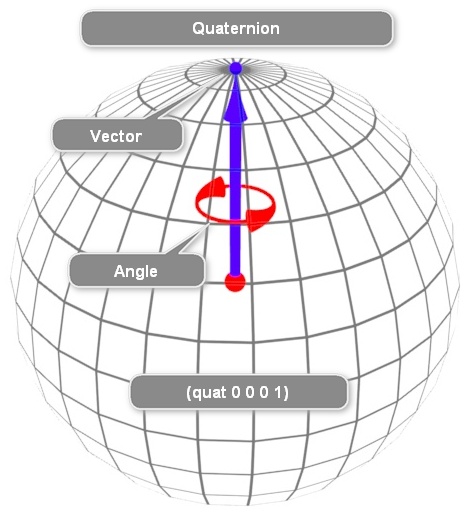
따라서, 실제 게임 엔진에서는 로드리게스 회전 공식과 동일한 기능을 제공하면서도 행렬로 변환이 용이한 사원수(Quaternion)를 사용한다.
'게임 수학 > 이득우의 게임 수학' 카테고리의 다른 글
| 원근 투영 변환의 원리 (2) | 2023.05.13 |
|---|---|
| 삼중곱(Triple product) (0) | 2023.05.12 |
| 백페이스 컬링(Backface Culling) (0) | 2023.05.10 |
| 외적(Cross product) (0) | 2023.05.09 |
| 오일러 각에서의 회전 보간 (0) | 2023.05.08 |

