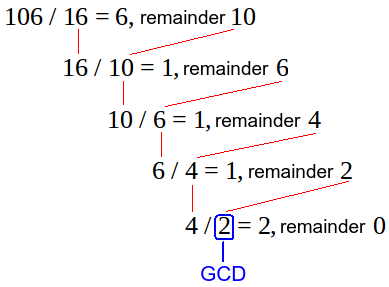
최대공약수(Greatest Common Divisor)를 구하는 알고리즘 중 하나이다.
유클리드 호제법은 다음의 성질을 이용한다.
// a를 b로 나눈 나머지를 r이라고 할 때
r = a % b
// a, b의 최대공약수는 b, r의 최대공약수와 같다.
GCD(a, b) == GCD(b, r)
의사코드로 나타내면 다음과 같다.
GCD(a, b):
if b == 0
return a
else
return GCD(b, a % b)
C++로 간단하게 작성할 수 있다.
int GCD(int a, int b)
{
return b ? GCD(b, a % b) : a;
}
최소공배수(Least Common Multiple)는 다음과 같이 구할 수 있다.
// a, b의 최대공약수를 G라고 할 때
G = GCD(a, b)
// x, y는 서로소인 소수
a = Gx
b = Gy
// a, b의 최소공배수는 Gxy이다.
LCM(a, b) = Gxy
G * LCM(a, b) = GGxy
G * LCM(a, b) = ab
LCM(a, b) = ab / G
C++로 작성하면 다음과 같다.
int LCM(int a, int b)
{
return a * b / GCD(a, b);
}'자료구조 & 알고리즘 > 기타' 카테고리의 다른 글
| multiset, multimap에서 1개 원소만 삭제 (0) | 2023.02.19 |
|---|---|
| vector에서 중복 원소 제거 (0) | 2023.02.07 |
| std::count 잘 사용하기 (0) | 2023.01.27 |
| for_each와 transform (0) | 2023.01.21 |
| 값의 범위를 제한하는 clamp 구현 (0) | 2023.01.19 |
