Level 0. 구슬을 나누는 경우의 수
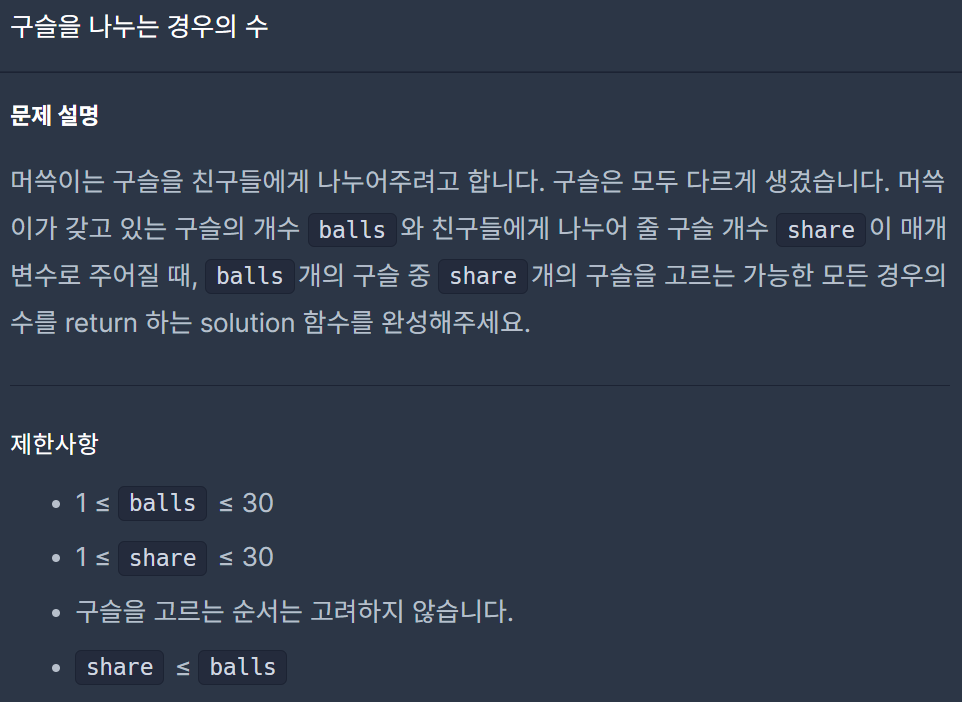
처음에 아래와 같은 코드를 작성해 일부 케이스를 해결하지 못했다.
질문하기에서 힌트를 찾아보니 unsigned long long으로 해도 범위가 넘어간다는 것이었다.
#include <iostream>
using namespace std;
using ullong = unsigned long long;
ullong solution(int balls, int share)
{
ullong denominator = 1;
ullong numerator = 1;
for (ullong i = 1; i <= share; ++i)
{
denominator *= (balls - share + i);
numerator *= i;
if (denominator % numerator == 0)
{
denominator /= numerator;
numerator = 1;
}
}
return denominator;
}
그래서 큰 수부터 작은 수로 계산하는 것이 아니라 작은 수부터 큰 수로 계산하게 바꾸니 정답으로 처리되었다.
#include <iostream>
using namespace std;
using ullong = unsigned long long;
ullong solution(int balls, int share)
{
ullong denominator = 1;
ullong numerator = 1;
for (ullong i = 0; i < share; ++i)
{
denominator *= (balls - i);
numerator *= (share - i);
if (denominator % numerator == 0)
{
denominator /= numerator;
numerator = 1;
}
}
return denominator;
}
풀긴 했지만 더 좋은 방법이 있을 것 같아 다른 사람들의 풀이를 봐보았다.
double이 unsigned long long보다 표현 범위가 넓다는 것을 새로 알았다.
심지어 매번 약분을 해 주지 않아도 될 정도라니..
#include <iostream>
using namespace std;
using ullong = unsigned long long;
ullong solution(int balls, int share)
{
double answer = 1;
for (int i = balls - share + 1; i <= balls; ++i)
answer *= i;
for (int i = 1; i <= share; ++i)
answer /= i;
return answer;
}
고등학교 때 분명히 알았었는데 어느 순간 까먹고 있었다.
10개 중 6개를 순서 없이 뽑는다고 할 때, 1개를 미리 빼놓고 5개를 뽑는다고 하자.
그러면 경우의 수는
- 빼놓은 1개를 필수로 포함할 경우 9개 중 5개를 뽑는 조합
- 빼놓은 1개를 무조건 배제할 경우 9개 중 6개를 뽑는 조합
즉, 조합은 아래의 성질을 만족한다.
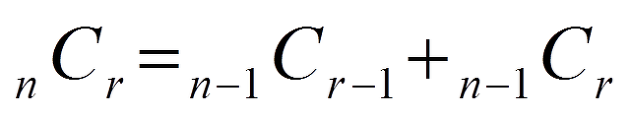
위 성질을 이용한 가장 간단한 풀이라고 생각한다.
Amazing..
#include <iostream>
using namespace std;
int combination(int n, int r)
{
if (n == r || r == 0)
return 1;
else
return combination(n - 1, r - 1) + combination(n - 1, r);
}
int solution(int balls, int share)
{
return combination(balls, share);
}
마지막은 조합의 성질을 이용해 동적 계획법(Dynamic Programming)으로 해결한 풀이이다.
재귀와 다르게 콜 스택이 쌓이지 않아 좀 더 효율적이라고 생각한다.
#include <iostream>
#include <vector>
using namespace std;
int solution(int balls, int share)
{
// nC0을 1로 초기화하기 위함이다.
vector<vector<int>> comb(31, vector<int>(31, 1));
// i가 5일 때
for (int i = 1; i <= balls; ++i)
{
// 5C1부터 5C4까지 계산한 후
for (int j = 1; j < i; ++j)
comb[i][j] = comb[i - 1][j - 1] + comb[i - 1][j];
// 5C5에는 1을 적는다.
comb[i][i] = 1;
}
return comb[balls][share];
}'자료구조 & 알고리즘 > 프로그래머스' 카테고리의 다른 글
| Level 0. 유한소수 판별하기 (0) | 2023.02.08 |
|---|---|
| Level 0. 소인수분해 (0) | 2023.02.07 |
| Level 0. 다항식 더하기 (0) | 2023.02.05 |
| Level 0. 분수의 덧셈 (0) | 2023.02.04 |
| Level 0. 겹치는 선분의 길이 (0) | 2023.02.03 |
