코딩 테스트를 위한 자료 구조와 알고리즘 with C++
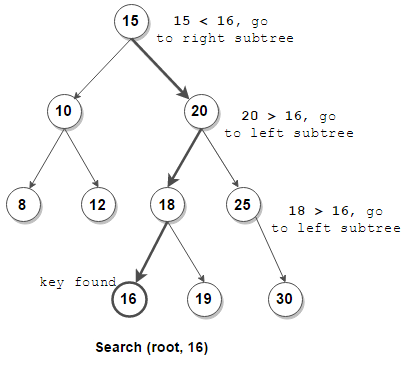
이진 탐색 트리(BST)
- 왼쪽 자식 <= 부모 <= 오른쪽 자식의 값 관계를 갖는다.
- 따라서, 중위 순회하면 정렬된 상태를 확인할 수 있다.
- 마지막 레벨을 제외한 모든 노드가 두 개의 자식을 가질 경우 트리의 높이는 logN(밑이 2인)이 된다.
이진 탐색 트리의 성능
- 하나의 레벨을 지날때마다 검색 범위가 2배씩 줄어든다.
일종의 업 & 다운 게임과 유사하나 항상 정확하게 2배씩 줄어드는 것은 아니다. - 그러므로, 검색 및 삽입/삭제는 O(log n)의 복잡도를 갖는다.
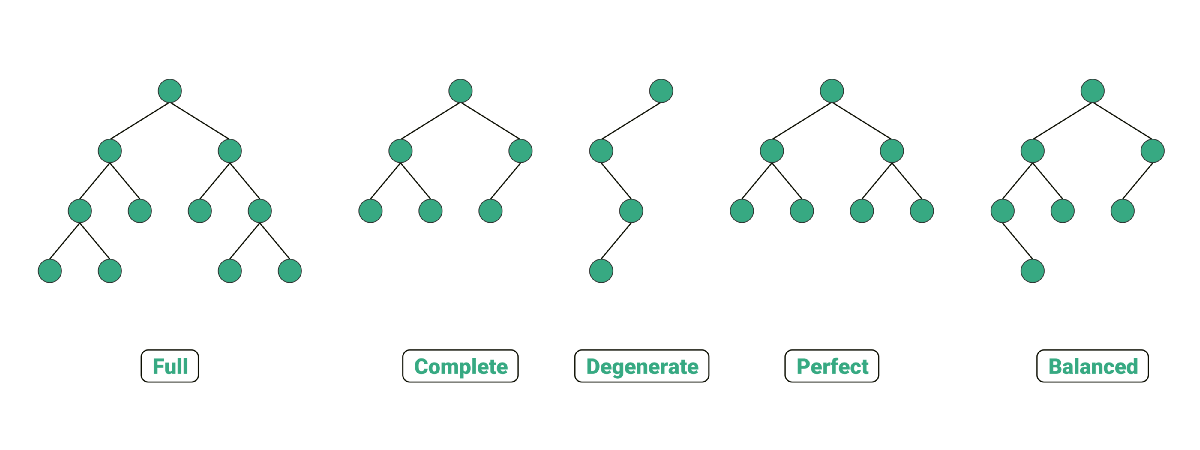
완전 이진 트리(Complete Binary Tree)
- 마지막 레벨을 제외하고 모든 레벨이 채워져 있으며, 마지막 레벨의 모든 노드가 가능한 한 가장 왼쪽에 위치한 트리이다.
- 높이가 h인 CBT의 노드 개수는 2^h 이상 2^(h+1) 미만이다.
포화 이진 트리(Perfect Binary Tree)
- 모든 내부(Internal) 노드가 두 개의 자식 노드를 가지며, 모든 단말(Leaf) 노드가 동일한 레벨을 갖는다.
- 포화 이진 트리도 완전 이진 트리의 하나이다.
- 높이가 h인 PBT의 총 노드 개수는 2^(h+1) - 1개이다.
검색 의사 코드
find(p, value):
if p == null
return null
if p->data == value
return p
if value < p->data
return find(p->left, value)
else
return find(p->right, value)
삽입 의사 코드
insert(p, value):
if value < p->data
if p->left == null
p->left = new Node {value, null, null}
else
insert(p->left, value)
else
if p->right == null
p->right = new Node {value, null, null}
else
insert(p->right, value)
삭제 의사 코드
delete(p, value):
if p == null
return null
if value < p->data
p->left = delete(p->left, value)
else if value > p->data
p->right = delete(p->right, value)
else
if p->left == null
node_ptr np = p->right
delete p
return np
if p->right == null
node_ptr np = p->left
delete p
return np
node_ptr succNode = successor(p)
p->data = succNode->data
p->right = delete(p->right, succNode->data)
return p
구현 예시
#include <iostream>
using namespace std;
struct node
{
int data;
node* left;
node* right;
};
struct bst
{
node* root = nullptr;
node* find(int value)
{
return find_impl(root, value);
}
private:
node* find_impl(node* current, int value)
{
if (current == nullptr)
{
cout << value << "을(를) 찾지 못했습니다." << endl;
return nullptr;
}
if (current->data == value)
{
cout << value << "을(를) 찾았습니다." << endl;
return current;
}
if (value < current->data)
return find_impl(current->left, value);
else
return find_impl(current->right, value);
}
public:
void insert(int value)
{
if (root == nullptr)
root = new node{value, nullptr, nullptr};
else
insert_impl(root, value);
}
private:
void insert_impl(node* current, int value)
{
if (value < current->data)
{
// 빈 노드를 찾았으면
if (current->left == nullptr)
current->left = new node{value, nullptr, nullptr};
// 아직 못 찾았으면
else
insert_impl(current->left, value);
}
else
{
// 빈 노드를 찾았으면
if (current->right == nullptr)
current->right = new node{value, nullptr, nullptr};
// 아직 못 찾았으면
else
insert_impl(current->right, value);
}
}
public:
// BST를 중위 순회하면 오름차순으로 나타난다.
void inorder()
{
inorder_impl(root);
}
private:
void inorder_impl(node* start)
{
if (start == nullptr)
return;
inorder_impl(start->left);
cout << start->data << " ";
inorder_impl(start->right);
}
public:
// 좌측 서브 트리 중 가장 큰 수를 후속 노드로 삼아도 된다.
node* successor(node* start)
{
node* current = start->right;
if (current == nullptr)
return nullptr;
while (current->left != nullptr)
current = current->left;
return current;
}
public:
void deleteValue(int value)
{
root = delete_impl(root, value);
}
private:
// value를 갖는 노드를 삭제하며 부모 노드가 가리켜야 할 노드의 주소를 반환한다.
// 값을 찾는 도중에는 start를 그대로 반환하므로 사실상 가리키는 주소가 바뀌지 않는다.
node* delete_impl(node* start, int value)
{
// value를 찾지 못했다.
if (start == nullptr)
return nullptr;
// value를 찾을 때까지 이동한다.
if (value < start->data)
{
start->left = delete_impl(start->left, value);
}
else if (value > start->data)
{
start->right = delete_impl(start->right, value);
}
// 현재 start 노드에서 value를 찾았다.
else
{
// 자식이 없거나 오른쪽 자식만 있을 경우
if (start->left == nullptr)
{
// 부모 노드를 지우고
node* p = start->right;
delete start;
// 부모 노드인 start가 가리킬 새로운 주소를 오른쪽 자식으로 한다.
return p;
}
// 왼쪽 자식만 있을 경우
if (start->right == nullptr)
{
// 부모 노드를 지우고
node* p = start->left;
delete start;
// 부모 노드인 start가 가리킬 새로운 주소를 왼쪽 자식으로 한다.
return p;
}
// 양쪽 자식이 모두 있을 경우
// 우측 서브 트리에서 후속 노드를 찾는다.
node* succNode = successor(start);
// 값을 찾은 start 노드의 값을 후속 노드의 값으로 대체한다.
start->data = succNode->data;
// 후속 노드를 제거한다.
// 우측 자식에서 시작하는 이유는 우측 서브 트리에서 후속 노드를 찾았기 때문이다.
start->right = delete_impl(start->right, succNode->data);
}
// 값을 찾는 중에는 start를 그대로 반환하여 부모 노드가 가리켜야 할 주소가 바뀌지 않도록 한다.
return start;
}
};
void main()
{
bst tree;
tree.insert(12);
tree.insert(10);
tree.insert(20);
tree.insert(8);
tree.insert(11);
tree.insert(15);
tree.insert(28);
tree.insert(4);
tree.insert(2);
cout << "중위 순회: ";
tree.inorder();
cout << endl;
tree.deleteValue(12);
cout << "12를 삭제한 후 중위 순회: ";
tree.inorder();
cout << endl;
tree.find(12);
}
출력
중위 순회: 2 4 8 10 11 12 15 20 28
12를 삭제한 후 중위 순회: 2 4 8 10 11 15 20 28
12을(를) 찾지 못했습니다.'자료구조 & 알고리즘 > 코딩 테스트를 위한 자료 구조와 알고리즘 with C++' 카테고리의 다른 글
| 그래프(Graph) (0) | 2023.02.06 |
|---|---|
| N-항 트리(N-ary Tree) (0) | 2023.02.04 |
| 트리(Tree) (0) | 2023.02.01 |
| 벤치마킹 (0) | 2023.01.31 |
| 비선형 문제 (0) | 2023.01.30 |
