Level 3. 징검다리 건너기
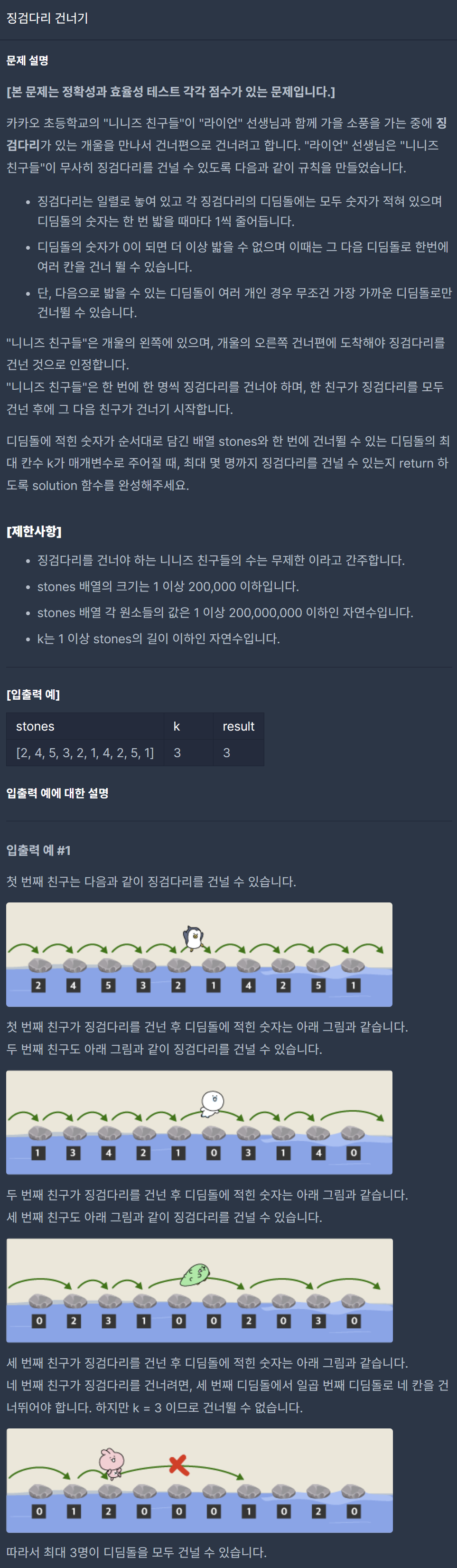
문제 자체는 간단하다.
k개의 디딤돌을 가진 모든 구간 중에서 가장 빨리 모두 0이 되는 구간을 구해, 그 구간에서 최댓값을 구하면 된다.
- k개의 디딤돌을 가진 각 구간의 최댓값을 구한 후, 그 중 최솟값을 구하면 된다.
O(n)에 수행되는 로직이고 굳이 따지자면 kn에 수행되는 코드인데 시간 초과가 발생했다..
// 이 풀이는 시간 초과가 발생한다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;
int solution(vector<int> stones, int k)
{
int answer = INT_MAX;
for (auto it = stones.begin(); it != stones.end() - k + 1; ++it)
answer = min(answer, *max_element(it, it + k));
return answer;
}
매 구간마다 최댓값을 구하지 말고 앞의 원소를 1개 빼고 뒤에 원소를 1개씩 더하며 최댓값을 구하면 중복을 줄일 수 있을 것이라고 생각했다.
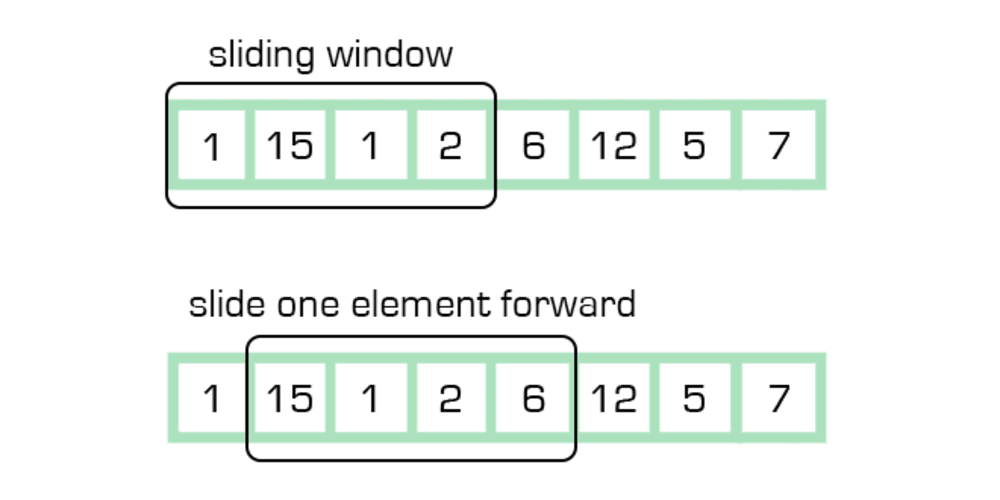
그러다 새로 알게 된 것이 슬라이딩 윈도우 알고리즘이며, 특정 길이의 구간을 뒤로 이동시키며 어떠한 처리를 할 때 유용한 방법이었다.
- 투 포인터와의 차이점은 양끝에서 가운데로 구간을 좁히는 것과, 일정한 구간을 가지고 끝까지 이동하는 것이다.
슬라이딩 윈도우 알고리즘(Sliding Window) (feat. 투 포인트)
1. 슬라이딩 윈도우 알고리즘 (Sliding Window) ( 슬라이딩 윈도우 알고리즘 간단 예제 ) 1, 2, 3, 4, 5, 6, 7 로 이루어진 숫자 배열에서 A[i] + A[i+1] + A[i+2] 형식으로 연속적인 3개의 숫자의 합의 최댓값을
ji-musclecode.tistory.com
슬라이딩 윈도우는 구간합을 구할 때 유용하지만, 이 문제는 구간 최댓값을 구해야 하므로 인덱스를 함께 저장하는 우선순위 큐를 사용해야 한다.
최대힙으로 구성하고 최댓값을 뽑을 때 현재 구간 이전의 원소이면 제외해주면 된다.
- 현재 구간 이전에 있던 작은 원소들이 힙에 잔존해있지만, 최댓값이 아니므로 알아서 제외된다.
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
struct Stone
{
int idx;
int step;
friend bool operator < (const Stone& A, const Stone& B) { return A.step < B.step; }
};
int solution(vector<int> stones, int k)
{
priority_queue<Stone> maxHeap;
for (int i = 0; i < k; ++i)
maxHeap.push(Stone {i, stones[i]});
int answer = maxHeap.top().step;
size_t n = stones.size();
for (int i = k; i < n; ++i)
{
while (!maxHeap.empty() && maxHeap.top().idx <= i - k)
maxHeap.pop();
maxHeap.push(Stone {i, stones[i]});
answer = min(answer, maxHeap.top().step);
}
return answer;
}'자료구조 & 알고리즘 > 프로그래머스' 카테고리의 다른 글
| Level 2. 시소 짝꿍 (0) | 2023.08.05 |
|---|---|
| Level 2. 호텔 대실 (0) | 2023.08.04 |
| Level 2. 롤케이크 자르기 (0) | 2023.08.02 |
| Level 3. 불량 사용자 (0) | 2023.08.01 |
| Level 3. 여행경로 (0) | 2023.07.31 |
